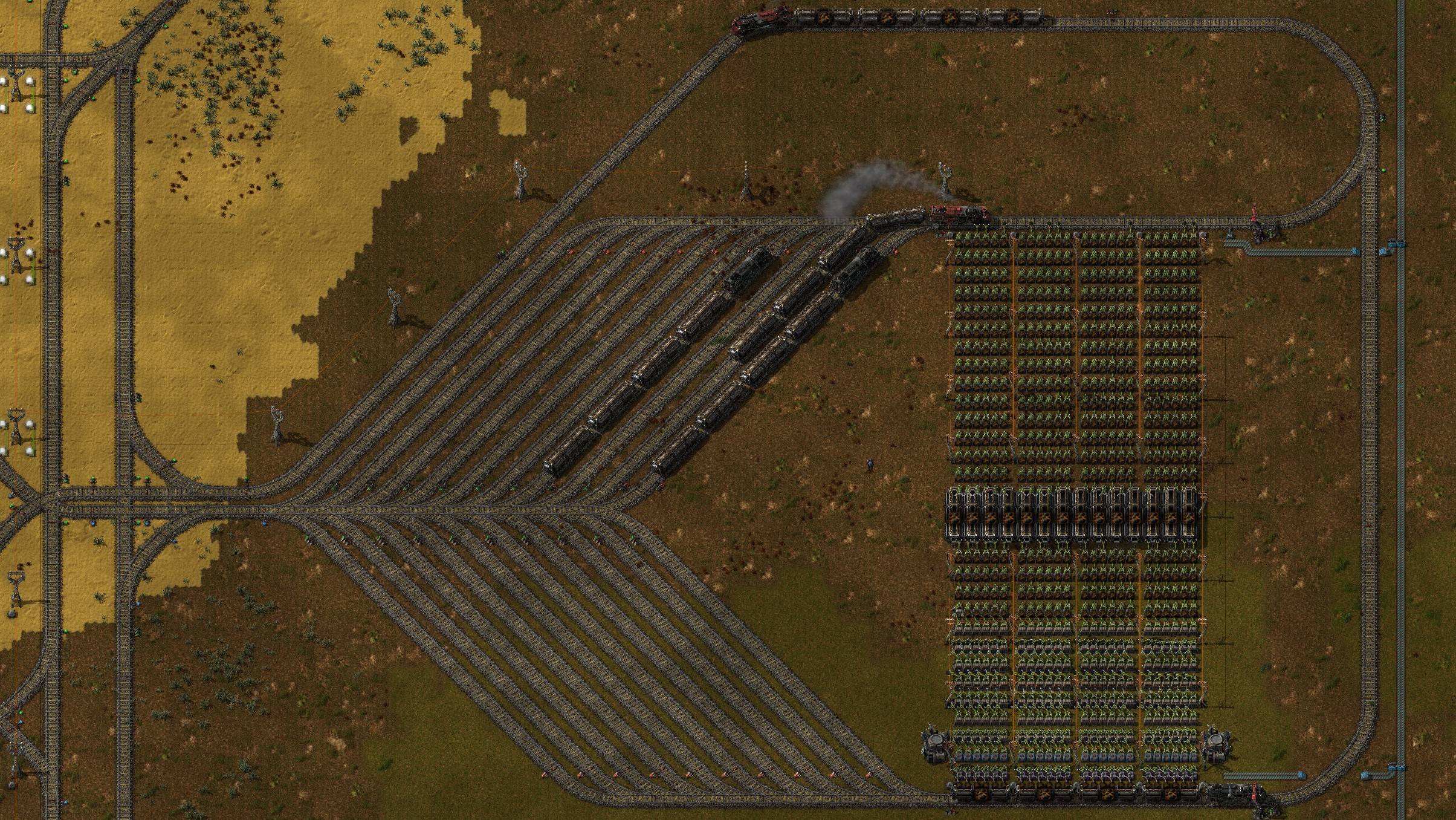
I see many people trying to figure out how to do efficient storage and buffering. I want to showcase a solution I and my friend came up with:
See it in action: https://gfycat.com/UnawareNiceFluke
To get high throughput, we had to solve a little problem. Train tracks are spaced in 2x2 blocks, and an inserter+chest is also 2 blocks. That means that if we alternated between inserter and chest, we would end up with a chest next to the train. Long handed inserters and belts are very slow, so we needed to break the pattern with a container with an even side length. We almost gave up until we found the following trick (we are probably not the first, but we haven't seen it anywhere):
With this trick we can load and unload trains at the max speed of 24 stack inserters (I will let you guys do the numbers). We call these things hubs, and we have many of them for different products. Advantages we enjoy from this:
-Decoupled production and consumption of common products (publish/subscribe pattern). We don't have to change the routes of consuming trains when production is scaled up or moved.
-Simple and timely indication of insufficient production. Consumption can go on unimpeded for a long time while we scale up production.
-Crazy storage space. It will hold a few million of whatever you put into it (depending on stack size).
blueprint
The blueprint is of the basic version of what is shown above. The upgrades we made are filter inserters and a primitive balancing system (a row of provider and requester chests).0eNqdnduuHdeRZf+Fz6KR677Sv1IoNGSJUBEt0YJEGW0U9O9NWjwXSjsyx4i3qm571IxIrsx9ZsSK+N83//jxt3c///L+w8c3f//fN++/++eHX9/8/b/+982v73/48O2Pn//fPv7753dv/v7m/cd3P7355s2Hb3/6/L/98u37H9/8/s2b9x++f/f/3vy9/P7f37x59+Hj+4/v3/3x3//P//Lv//Pht5/+8e6XT/+Br/6bb7/Qv3nz8z9//fTf+eeHz/+HPnHetr+Nb978+9P/0Mffxif+9+9/effdH/+B+vs3f8FWhm0S256x3/32y7/eff/2P+H+Ve36Am1fI+cDZH9G/vrxE+2H//kYQesXaL/XOSj04MxJmULnoszOmZsyJ2eelLk5sxwUWsRTKgVTxXMqFVPFkyoNU8WzKvhEFfO08JGq5mnxQ2WeFj5W1TwtfLCqeVr4aFXxtCo+W008rYrPVhNPq+Kz1cTTqvhsNfG0Kj5bzTwtfLa6eVr4bHXztPgnyzwtfLa6eVr4bHXxtBo+W0M8rVbYT6sxHv+0ao+Y+GS9ff7EHl9j1yMsPlpjP6aWR1T+Q/Dpy902EDs09s9qH6Z2ssc1yxep6/dHlMXFfTlNbYKYt8duEPPJsV9Oaev3avvhsfNebS8c++WfaatAbfXYDtQ29gfbfP6D7fOfbl9z+yOu+PPqyyuggVdAHx5bQRbkqarn18zxiInP2KzPSh9x+KF6+q1awfupnxrbwPtpHDrq41HUg5+ip9/SFbyhRvVY8IYazUb9ifqI078+jd/9z7fvP4AzWRc5k+Pl8Pzj/Q9v3/346T/8y/vv3v78zx/fPUrA+QU+HkqdPJNf3p4VvJTH8ljwUh5bhb4uIz8Nq4wr1jzcr6/agF9U7M8kksFZ9T/x+TDixh/wkzzweZzdY8HncQ4ddX8YNT8tT38YV/A5nMtjwedwbmi31qd/luXeb50nhRYOXYf+PfDnBDy0R+EfRW/LElr9LziktemfsQjbaQqaSMHQfyAgrVP/rYWwC6bgFBnY+k9jJJX/mhP/tDb8Or0Vr4HNf9iJf62bny3x72rTspN4Y21dd0JKbeEJQeFfReIFsJcsZiGdW1azEBR+rsQH4DxkhYzoPIsskSFoZcEX8Q//bLbshpR2W3ZD1GHLbog6bdkNUZctuyHqtmU3RD1t2Y1Qy3HYuhvDFlt4Y9hqK28M22zpjWG7rb0x7LDFN4adtvrGsMuW3xh22/obw562AIewvG+im0fGGye6eWS8c6KbR8ZbJ4Z5ZLx3Yr48socg/hfW03ktwC0uZWpuBXZxKUv7Nkzv1kYv457acEDc6otRjFv0n8aMW+0fnAzb7N9xDNvln0eMOuTfHYw65Q96Rl2szlf6c03h+HNNYT4Evz5o7959rlm8+/Xjo5+0T+By/u2hF16+apv49rv/+/b9h1/f/fLx0//fBe2vMvvDjrcDyty3MluBqHWPqjzibSNunL0su7MUfMbdpWDAbJ73qIkjfhFGI148m6dlwyNUy30K+BF6oUGZHR6h2m9ldniEartH8SNUu42YH6EXpZRNj9D9e7PDI1THPUocIfsK7vwIvSil7M3Z9kXaxZmyL9JBz9T9Z2nQM3X/WRr8TDX7Iv2qVeJCZrv/dIzOZVYrc3C2fZF+1TpxlYJ6n4IFUfefjsGPULMv0sGPULMv0gmPULv/LE14hNr9Z2mKI2RfdpMeofv3/RRHyL43pzhC9r056RG6f29OeoTu35uTH6Fu35tTHCH7A3TBI9Tv38mLHqH7n/OLH6FuX++L/7Lr9vW+4C+7fv96X/CXXb9/vb/qkfjsKnx4++vHf/584Voe5LoTNBVGkaYC75KYL2bjQxC3657qDAW0kZZXnRE312dfvjr7z6GXh+TiFYMO1SI6JJ7qQywTzXOR3q4bQZneYVps37768+svz2885Pu+WJaPpfu1WT62y0e1+fB95igf56G76VA+zqLy8covZPk4fRcgy0fTrXUsH93lo9t8+JZAlo+pG+1YPpbLx2Hz4RsEWT5O23dH0lGPQ6VDvk3robsFSTLqUW0THktGc+9SmwzdOsiSMWRPHsvFNLkoNhW2j5Blwo6wYJk4TSaGzESxTYUoE0V9BU+ruSYKfX9l94fspuuR6/GfTPVVU8ZP775//9tP93d97pkjUfGjoc9ExY+yly56hinYuhQbos5EVQ5G/FVHBq0mUnbRRc8oBV81YrBSbIhqieIhjbjrGmcoc8hj+epvlpA5E1VEGvpKVBEpe+tCapiCU5d3IxRttqj372DabFHvX72i2aLar45otqjDsnui/kjZI1E3peypC5Lho1u6TBqidqK2SSM+dW0zkvmq2QK+5O4/FV91XdB6KQxdtGE0++3oTRc5wxR0XXoNUSNR06QRz0QtlrKXLnKGKdi69BqizkS9FEZMmyza/TfkVZMFO5bt/hNnui3s+320RH2XsrsunIYpGLqcG6Jmok5KI16J+i5lb104DVNw6nJuhJpHok4KI54lUd+l7KoLp2EKmi7nhihrKPT7d7CfUFH2Y5C44fFkJYGBLtXMqAhstYcW1dz+pgvSe3ou0WtGVWyhdxXPRXr9qCSmt3ku0usnjjG9fuQY0zv9jR+kd3ku0rv9TSKk9/Rconcf+oYSkSv6M8xp8wMsmFp/nwqp1fepkFg7xIJpnfaWFtJqJ6gzrf4y1Qh+F+zMZarP/xP4dXX6y1SRzLNk6iFQZs3UQyC76XpImAJ/mSpE+ctUIWpmSisweStTWoFsf5kqTEHmMhWT2Q5/mSqQ2Q5/mSpEZS5T0Ygzl6ko21+mClPgL1OFqMxlKhpx5jIVZW/ttocpOHUNIEKVI1MGYRGXkimDQHbVRYEwBS1Tu4AyvTMeyhzarw9RM1OygBGvTMkCsr0zHqbg1H59hBItDc2+gmvJlCwgu2oDP0xBy9QZoMyuXexQ5tDeeoiamfICjHhlyguQvbWLHabg1N56hGpHprzAIm4lU16A7Kpd7DAFTXvrIapnygsw4pEpL0D21Kb7fJwAYY4/2UmVbErZngvGYbeWuE9F9IpdHK0LvWIZx/PtJKQ3cZsK6W3+9hDSm7hNhfQOf7sH6Z2ei/Quf/sG6d2ei/Se/nYM0TsOzyV6xdqOYs7b8BulmN6m75cguV1jkdqhL4AgtVNjkVp9RwOJ3ZaKtKbc8o5+LNABFa/ALfi9NFNuOZSZcssh27vlYQq6rj2EqKGN9xA1tfEeojKTxuhz2BnjHbJPbbxHKVhHxnhnMumAilf+diizauM9RLWM8Q4j7hnjHbKHNt7DFExtvIeolTHeYcQ7Y7xD9qmN9ygF+9DGe4gqGeOdRbxrxniHbD9pLExBzxjvUObQxnsoc2rjPUStjPEOI94Z4x2yT228RymgXQ7t/vUuuhyafQWLLodmPx2nnzQWpqBnjHco07ePhzKnNt5D1MoY7zDinTHeIdu3jwcp6LTLoZ33qJIx3lHEXbQ99MOyfft4mIKujfcQNTLGO4x4Zox3yNZLdUt/nAC3ELR/2XFVymMat+meNnkUsu2YD3d44ZJ1x6X4nnykt3ou0tt8Tz7S2z0X6R2+Jx/pnZ6L9C7fk4/0JrZwIL2JLRxEb/XrRJFes4XDnDexhaOY8ybWcBRz3vgejhcu0jt0Uz6SOzUWqV26KR+p3RqL1J62K5+IbYelEq2ig+KV217RTw/aQfEKXIJfX2Y1x7Yye8bGh+yhbfwwBVPb+CEqZZjDiFOGOWSfumYQpQCv5jjuUUXb+CGqZmx8ljw6E+KVWx7K7NrGD1EjY+PDiGfGxofslGEO2SnDHLJPXX6IHh3exDHuUUXb+CGqahs/RLWMjc+eg9jEUe0HDc+GuH+3mdkQ9m2e2MQRytwZ7x3KPDPeO2PjTRz1NgV4E8f9652Ogmj3r/fZMjY+TF7P2PiQPbSNH6ZgZmx8KHNpGz+UubWNH6LOjI3PIhaNDs2+N1fKMIfslGEO2U3XDKJHhzdx3H86VsowhxGnDHPIXrpmEKZg60pGiDq1jf9w3XEXQx6edl2DbaldDHnogf/10J8wSzi2kNt8tz+S23VXPpI7fLM/kjt1Uz6Su3yvP5K7dU8+knv6Vn8iVyzcqOKoncV3+iO5fs8Gktt8oz+S23VDPpKb2K6B5PrtGkju8m3+SO62/fhIrV+pAcSO47Dt+EDsEJs0qhGbGuWPFqmNQ4/yD5afjSM/yT9Eai88JGkrPCStTF0BPoydqStAtnbCowyIIRGvbHWm0gyJOCxbT/EPM9Csfx+Sesa+h/HmZ/iHcqetCISklXHxYeA74+JD9mkLGVEGqh7gH5L0/P6QlBrfzzJXU+P7IbvbakCYgWGLASFpZmoBMN6VqQVA9ra1gDADZ6YUwFS2/Oz+SC5dg9FuX5O0jaHdfh9EF8Mrxx+msGfKFJCdGtwP2anB/ZC9bE0kfHLblkRCUmpsP4u367H9kcqen9ofIlND+2HgqaH9kK2H9ocZ0JcuQlJqZD+MNzWyH7L1yP4wA/rKRUQaqYH9LN6RGtgP2Xpgf5gBfeEiJOXH9YdIP63/eAziBlz/YuyBXZVjLI0F6yTH2PoeA1Lrr10QtfPQtxiI2ukvXSC1Vd9hQGr9lQuktusbDEitv3CB1E59fwGp9dctkNqtby8gtf6yBVEr9mEUccqWv2qB1FZ9cwGp9RctkNpuLy4gsfqWBdI67bUFpFXfsUBad6LagTYWDTr74YUbbAQadPTDi00fkoqtTISkmqhMsMTtlihMQLSezB/Grwfzh6TMXH4YbmYsP0Trqfxh/Jmh/EzkqWfyRyJPPZI/JGUm8sNwMwP5IVrP4w/j1+P4Q1JmGj8MNzOMH6L1LP4wfj2KPyDNIzOJH4U7j8wgfojWc/jD+DNj+KFIPYU/FDkS7jwUORPmPETrWxRh/HoCf0g6E/UCFq5oV2hdoov1+KP4S014/FCkni8UitSz90OSHr0fkjKT92HiMoP3IVrP3Q/j12P3I1LNTN1n4dbM0H2I1jP3w/j1yP2QlJm4D8PNDNyHaD1vfz+OXrgCX8whsAxwmskLj62s9hB76lsIRG3zdyaI2lb0JQSk1l+ZQGqbvoOA1PobE0jt0FcQkFp/YQKpXfoGAlLr70sgtae+gEDUdn9dgqgVCy2KOGXd35ZAapu+foDU+ssSSO3Qtw+QWn9XAqld9vYBEqtvSiCt2twONgZN0d/wAkNLfSYd2/DiIociM243FJlxuyFaT9YP49eD9UOSnqsfkjJTgmDiMkOCIDrjdjM0ndbwwo1SK7ZSvHjUUGRNeNQQ3axHH8bfbd0gJOlx+iFJT9MPSZnZQPARZEYDQbQepR/Fv/Qk/ZCUGaTPwl2ZOfoQrcfoh/FnpuhDkXqIfihSz9APSZkR+jDczAR9iNYD9KP4d2bbLBO5M8tmIVqPCwrj1+Z2SMrMzofhjoRHDdEz4VFD9LIefZjabesGIUn3cEekU0/ND0mZGUDsEZyZEUAQrTu4w/gzbjcUmXG7IXpatz+MX4/Ln485wuD+Yg+BXX5TDFDoj82sR27DEgMUnprYgdolJij0LtRW3cSO1DaNRWq7bmJHaofGIrVTN7EjtUtjkdqtm9iR2lNjiVqxm6KKUyZWU1RxysRmiipOmVhMUcUpE3spijhlYi1FEadMbKUo4pSJpRRFnDKxk0IcMrGRQpyxmnG70SadRQczvHCDXUKLtjm8+NEhqVkHOiT1hAMPEzcSDjxET+ubh/Ev65uHpJ3wzWG4Z8I3Z+imze0ofrFS4gUGRVbrG4ciM+tjocjM9liIHtaBD+Of1jcPSRm3G4abcbsh+rRufxQ/3iRx+wruGbebhdszbjdEN+v2h/F365uHpJHwzWG40/rmoUjduR2SMuPvYbiZ6fcMTfdHtNuX+cgsi4UiM7tiIbpZ3zyMv1vfPCSNhG8Ow53WNw5Fai87JO2Elw/DPRNePkPTPoR++57ESyNuf/SKtoMmf/SKHRJdvsxnxu2G6IzbDdHa7Q6f2rJ1g5C0rW/eH3O4KzD+sIfA7rwlJieMx17WQ7NBTE740sWOxFbdG4/ENtvEjsR23RqPxA7bw47ETt0Zj8Qu28KOxG7dGI/EnraDnYgVWyWaOGBiq0TlB0zslKjigImdEpUfMLFRoooDJjZKFH7AxD6JIg6Y2CdR+AET2ySKOGBim0ThB0zskijigJ2Z9a9oj846/fbX4LfFq+4GO4u+Rsiu97JGpKHXskakmXDg4bNYCQceojNuN0Rn3G6E3odf//r4qe2j6J20EanqPbIRqSUceJi4nh5DXyO1Qy+mjUgzYerDuFfC1IforbfpRvH75a4BSYxZqO67sM1SiCHRVW+kjeLXpnZI6glTH4Y7EqY+RE+9kDeKf+lltBFpJ0x9GO6Znj8fvdXMAIbq1IoBDE2+3quedR89LdqZ8GrQfUTqCXcfhjsS7j5ET71EN4pfT7EPSVtvtY1ImSn2LHF6F0Sbd2dRdCQ0+Q5uNWHzQ3TTG3mj+PWon5A0EjY/DHcmbH6IXnpBbhS/HvUTks5E6YGF249E6QGii16OG8Tf9aifkNTSQ+ejFwYflzCfPbeHHO6yjT9AoHNyi/EI46HR2B5Sl71agLTqexBI62kvFhCtQ9+CIFpHsdcKkFZ9BwJpbfZSAdKqb0AgrcNeKUBa9f0HpHXZCwVIq779gLSe9joB0Tr13QeiVSyIqPxsTX3zAWlt9ioB0qrvPSCtw14kQFr1rQekdSVKGGjFzp5bljCO4PcEna3wbL5HIDpa4blAEIJKotjAsiYmK7wUGyC6JYoNEN0TxQaItqPsw4dmbzuEoJUoEMBg7dz6UOOZMPOZRjFn4cV0h2g7xz4Kf9urDiGoJax8GGxPWPkQbafYh+Hbiw4haElLPARtWVsIQWeitMDSfx6J0gJEl4SND9F2YH2U2TOzqBVqzOxpheghzfswfHvHIQSthHUPg90J6x6iT2ndB+Gfh73hEIJKwm5HwZ54ycO409gSJjvU2BMmO0Tb2fVh+PZ6QwhaCYsdBrsTFjtE28n1UfjFXm4IQSVhsLNgxX6HXiXazq0Pw+/SXw9BdgHr8Rjzcj7+8f6HO4v+7WfH7N+f/+J/yOJ22vjDTAKDfE8x5mA8NL7aQ6q+0EC0Vn2hgWit+j4D0qrvMyCt+joD0qqvMyCt+jYD0qpvMyCt+jID0qovMyCt+i4D0dr0XQaitemrDEirvsqAtOqbDEirvsmAtOqLDEirvsiAtOp7DEirvseAtJ7eVi/oJw4dmPCMDar0Z0942FBiwsKGZDuwJwze3mAIQXb0fAiyk+dDUGLwPMx+Yu48JJ/S9o6CF+sanllMIt3W8OwohxKr9LhDUGIID4w1MYMHku3A+TB4O28+BCUG8MBYE/N3INkOm4+Cn4nNqkziTCxWheQqCwBh8Im1qlCiHcUTSrRj5kOQnTIfghJD5mHSEjPmITmxUJWRV2KfKiTbdarRA1tVuughqHkXHcZqB/CEEod0kUPQlL52CFre1odJ297Vh+TTW+iMLDoHunvjbjuKJ3pgtHGg3726ReNAd68z0TfQ3SuYtg30u68EbRvod9+tbQfK18eYl8Py3W+//Ovd96Hde/6Hsr5OVn3IFNb0Q0vqoXEgJhV86U6fwOQ4i6UirdV2pyOtzVKR1m6705HWYalI67Td6UjrslSkddvudKT1tFSgtRxiUUPDh+sTtlgsU1ttgzpT2yyWqe22RZ2pHRbL1E7bpM7ULotlardtU2dqT4tFaktiiHwjv08+oe0Q+f74d8UnUs1OxYmRTXrKMSkxTZ5mMDFNnqKnNOfj+Jc01WNSYr4ODTcxXwei6yFrAWH8NTFNnoq0A3dikS07FSdGdu+N07iHN8cpesrSQBz/ktWKmLSlYx+T7ND4kNQS83XgI2iJ+ToUbY3rOP7mbXsqsnvfnqKHrFrE8U/v3FORduBOLHJnp+LEyNOb7zBuMfWgyQ8FnXrQbj8UdOpBu/0+9OZLAjTc7msCFD1kUSCOf8qqQExavixAw7UDd2KRZ3YqTogUnQZNvoPNQgb5DqbNB+32G4T3L9y+zUW3QZO/0cVChi4/FHghw+1bnS5k6LefHNFx0OVLXCxk6PLTgxcy3H4f6EKGfvt9mDU7FSdGNlnK6AHn5bh8/q9/ivHb9x/e/vr+hw/fPnJu5lOsf9kFXB/jBy2V/HHH4ETQSaFNQPU9hknsq0lrRf0UWvU9BqT1Vf/BjdbBtfq9DExrpVqL0KrvMTCtHWpt4hD4rQxMKz1bTZwtv5SBaaVnq4qz5XcyIK2bnq0qzpZfycC00rNVxdnyGxmY1m4vBzDs8FWHwX6g0G6GZ+6MfgPs5Y19KnJ7Y5+i7fydMP7TDuCJScUb+zDcs3pjn6KbNPbj+LsskcSk4UsENNwpSwSxyOX9fCpyez+fok/p50fxF7xxod+SivfOWbjlqN47p+gmawdx/F3WM2LS8C48DXd6F56il6xCxPFv6efHpNP7+TBcOhCh3b0ni5iI8Ow/U5HVm+8U3aT5Hsffpfkek4Y332m405vvFL2k+R7Hv6X5HpMSg+RhuLQHod2+cWtifjwVmZgfT9HW347j79Jzj0mJ+fE03MT8eIq28+Pj+O38+JiUmB8Pw22J+fEUbefHh/E3Oz8+JllbewacP9naoaE9niStPydtPAYPCO5bgicFdwleFHxI8Ibg5/InBZ8ULB/eq7aEa3CVD+9VU8INWD68Vz0KN2D58F61LFyDi3x4omEhRj9+YfXh/S6Knt7voujEBAWKToxQoOjT+zgQbaYqdIku3n2h6OqdDopu3umg6MTGO4pObLyj6ERHHkUnbpxTdOLKOUUn7pxD9ExcOqfoxKRUiq7+r0CKbv6vQIpO9CZRdKI3iaKn/+uGopf/64ait/xLYj/+S0L0WnwBlQPUQ8vitwfnYbjFddyUAuqhZfHbg2Mbtc1ee4bc7lqEYBaG7RGCavUSMchdrvkIZmHb7iOo9rRXtRl3y7YmloWt+5qg2movgUNucw1TMAt6RitUO+z1csidrhULZmHZXiyoVl+Hh9zTNXmxLIhhE838yz31hXjIra59DGah2f4xqLbbi/aQO1xjGszCtJ1pUO1yrWlQLT5n5VnsYxD+hJV9Bap8tkQ9rkH48NR6DcLfpdqvQfiA1HkNwiei3iQbf2zaTbLxv/p2k2z8QWk3ycb/sttNsvG/7Had7IL/ZffrZBf8L7tfJ7ukb2eUYE/DJ6atY4Xi5P2M50Fnf5nRNR/z/Z80fxrbUR5zp/4jgXGX/tnNuFv/kGXcU/80RNzqf2wxbtE/XxhXD8eHXN1WDrm6rxxyh/2pUR+/GPjGiSd9EWjZnxoRaNufGhHotD81AhDfHlGvk80XRtTrZPMdEe062bxRol0nm2+CaDfJHvanRgSa9qdGBFr2p0YE2vanRgQ67c+CAIQ7Gcbz8Ny/3J9dj8l6uOOfX3zjMZd2MoxiFTeteJJXde/aj2SZwC1Ey2ZiasUsE0t7kiwTtIPo5Rc3zcSpFaNMjEP7kigTgzYQvcxIhpkYVStmmWjam2SZoJ17zb7ZxtCKWSam9idZJmjjXrNvzLG1YpaJU3uUKBMT9+3ZN+YsWjHKxKx20CjMBG3bq/aNOfXEVZiJYYeYwkzQftli35hTj12FmdBzV2Em9OBVpnclJq+Wjroz6sqsC6PszMIwym6JdViU3RMLsSg7cS0Xs2dicxRlr8TuKMreiV1NlH0mtjVB9s6sWaLszKIlyq6JDUmU3RKLhCi7J1YJUXbi8iJmJ24vYnZiTh9m78SWG8o+E3tuIPs8EptuKLskdt1Qdk3slqHsltguQ9ndmmmPZ6BVsXdjPP7B9/iH2elrYJv8MDt9DYzp3ZrL9J66tkb0NrGA44lL9DazgWMbvVVzmd6ma4FMb9dcpnfoGiPTOzWX6V26dsn0bs1lek9dE0V6eevGMxfp5Z0cz7VWprdqLtPb7JJvqLdrLtObGGZWJvoIt2KnmX3efPL7Y1RinBmWmZhnhtmnHEMWpwCv6lj3qMRIMxpxTcw0w+wmR5FdpKDL+WgXqIx/QiO2c80uZCYGm2GZiclmmH3KgWRxCtohp6RdoBLDzWjELTHdDLObHEp2kYIuJ6VdoBIDznDEiQlnmG1HnF2kwM44u0AlhpzRiLudchbL7IkxZ1hmYs4ZZttBZxcpsJPOLlAZt5BGnHELKdsOO7tIgZ12doFKjDujEQ877yyWORIDz7DMxMQzzG5yUNlFCrqcnnaBSgw9wxEnpp5hth17dpECO/fsApUYfEYjnonJZ5htR5/FKZh29tkFSl8amQHIdy5uYlCIXo4v3HoQg2JO3a3H9Oq+Rah36546pve0XKZXzJpoU+gVuz2+cKHeqvvTmN5muVCvv5vL9A7LhXqn7vViepflQr1bd2QxvaflMr370B1ZSK+YOVHMeRMzJ4o5b2LnRzHnbSdmDH52X8lPgz2sob2i7/mrBgy5FfyCmTHJaegZk5yytUkepuDUJnmMypjkMOLM4g/M1iZ5nAJtkseojElOI9YmeSxzZReEXzB3wninoZ8J452x+6Hd8igF/SjWw49RiVmbOOLEsE3MtttALlIwrPEeo2bCeKcRr4TxTtnaLY9TcFoPP0SVI2G8w4hLscZ7LLNm94VfMDNNtjT0TJMtZQ9r5scpmNbMj1ErYebTiHfCzKfs05r5YQrwVpD7T0ZNzJqlEddqzfxYZsuuDr9g9kSBgIY+EgUCyp62QBCnYNkCQYzaiQIBjfhMFAggm/Y9tPv3PF4Mcv8Zapnechpxprecsrt19eMUDFtriFEzPakqZi5bdNgBSHeP/9nsGY+5p+ZWYCL1rrvHmV4xQOOJy/Tq7nGot2ku06u7x6HeoblMr+4eh3qX5jK9unsc6j01F+kdunuc6R1Fc5le3T0O9TbNZXp19zjUOzSX6eXnrZjzNpbmMr3bFx0++6/k58Y4bdHhjL7nom3i2WunMsVCj2fzHbOrLRDEKWi2QBCjui8Q4IiHLxBg9rQFgjgFyxYIYtT2BQIc8WkLBKHMlVhQRWWuxIYqzK7WzI9T0KyZH6O6N/NxxMOb+Zg9rQMfp2DZukCM2t7MxxGf3syn7H1YBz5MwS62LhCjEiMpcMTNmvmxzO6NdyxzeOMds6c13uMULGu8x6jtjXcc8emNd8qmfQ/t/vV+Fmu8x6jqjXcccbPGeywzYZJjmQmTHLOndbbjFCzrt8eohEmOI06Y5JA9aLtDv30nD9ru0M57VMIkxxEnTHLM1iZ5nAJtkseoKQ3tegQg3z1egUExxNiHJy4ZLT8O3z2O9BY985bpLb57nOmtmsv0+u5xprdrLtPru8eZ3qm5TK/vHmd6t+Yyvb57HOkVqz2qOW/Vd48zvVVzmV7fPc70ds1levl5M8eNL/p4a06bGBXxYmdX9sOgbmlnfzblHn+ERcvEi50NZbYjYWdTdpF2dpyCVqWdfYFKjK/FESfG12L2kHb2RQqmtLMvUCthZ9OIt7SzL2SeCTsbyuxHws6m7CLt7DgFvUo7+wLVEnY2jbgn7GzKHtKDvkiBdcYvUCthZ9OId8LOpmzbUB6ngI6KqPdfCjMqwr6CR5V29oXMRB85lpnoI8ds20d+kQLbR36BSvSR44gTfeSYbfvI4xRM20d+gUr0kdOIp+0jv5DZEnY2ldkTdjZlD+lBX6TAOuMXqJWws2nEO2FnU/Yp7ew4Bcu2j1+gSsLOhhGL3R7dfjpoz0O/fyevLu3sC9SwdnYNQFP3JZP1M0MMfXjikvUzQwx9aNvo1Rt5md6tN/IyvWLowxOX6a26L5npbZrL9Hbdl8z0Ds1leqfuS2Z6l+YyvVv3JTO9p+Yiveeh+5KR3rNoLtNbdV8y09s0l+nl580cN7Fsw5y2cybsbLZoZNDGiRdwi77mrxon5EiY/4h9zMxY5Cz0eWQscsrWFnmU1nloizxGZSxyGnHGIqdsbZHHKdAWeYzKWOQ0Ym2RxzLP7EiY8FjOkukih6GXTBc5Zdsu8jitxXaRX6AyXeQ04kwXOWVrrzxOge0iv0BlushpxJkucsiu2isPU1CLdfBjVKaLnEZsu8gvZPbsSJj4JWfmQ1Qb+kxY+ZS9rJUfp3VbKz9GnQkrH0Ysmh2a/Rw1204ep4A2O7T7r49odmj2tU7nQ7T71/qr3gY5EiY+lmIfRrPvd9H10Oz7nXY9tPuXcjtteSBE9cRiTxpxTyz2xOxqywNxCpotD8SonigP0IhHojxA2dN6+nEKlq00xKidHQkTvz34BIj5bFw+BA3fOU4W5U0x8uGJSxblzeE7x5neprlMr+8cZ3qH5jK9vnOc6V2ay/T6znGm99RcpHf6znGkdxbNZXp95zjT2zSX6fWd40zv0FymV7eOM7nLYplacS/KqD0tFqkVQyJe6gJsPc1cxRYcop0yUzRMvPjsVGZLFAcou1tHP07BsHWGGDUTxQEa8UoUByh7W0c/TsFp6wwhah+J4gCMGA+JKPcya8LIpzJbwsin7G6N/DgFwxr5MWomjHwa8UoY+ZS9rZEfp+C0Rn6IOo+EkQ8jFssxqv10nNW673EKmq0JxKieMPJpxMMa+bHMmTDdqcyVMN0pe1vTPU7BaU33CLVEi0OTr+B1lITpTtnVmu5xCpo13WNUT5juNOJhTfdYZsYgpzIzBjlla4M8ToE2yENUyRjkMOKSMcgpu1pXO05Bs157jMoY5DTijEFO2dogj1OgDfIYta2ZPQOQ7xsnS/KWGPfwhdvIkrxVfd8401stF+r1feNMb7dcqNf3jTO903KhXt83zvRuy4V6fd840tsOy2V6m+8bZ3qr5UK9vm+c6e2WC/XqxnEmd0osVCtOm1G7JRaqPRNmNlulsvphzexoV8kSzRIvZi6VWRNmNmXbgeQXKejWzI5RI2Fm04hnwsymbDuQ/CIF25rZMepMmNkwYjwiotzKFCMiXsxcKrMmzGzKbtbMjlPQrZkdo0bCzKYRz4SZTdnLmtlxCrY1s2PUmTCzYcRiLUa1n46pW8nDFNAREfX+9W5GRNhX8OzWzI5lZjrIqcxMBzll24HkFynQvniMynSQw4hXpoOcsot1oMMULO2Lx6hMBzmNWHeQxzJHwsymMmfCzKZsu7XzIgXaF49RZ8LMhhGLjodu38nbDiSPU7B143iMagkzm0bcE2Y2ZduB5BcpmNbMjlF2WWfdAWjbjuRGlq8tMezhiUuWry0x7KFVoVcMe3jiMr3VdiRDvU1zmd5uO5Kh3qG5TO+0HclQ79JcpnfbjmSo99Rconcfh+1IRnr3UTSX6a2yJRnKbRbL1HbZkgzVDotlavFZO4zYJalMa2JJZ2PrTvZhl3TWaEfJLoklnVRmSSzpxGy7pPMiBdoTj1GJJZ044sSSTsy2SzovUqA98RiVWNKJI7ZLOmOZNTFehcqsifEqmK3Hq8Qp0ONVYlRivAqOODFeBbP1eJU4BXq8SoxKjFfBESfGq1B20+NVwhQ07YnHqMR4FRyxHq8Sy0ws6cQyE0s6Mdsu6bxIgfbEY1RiSSeOOLGkk7K7XdIZp6DrqSoxKrGkE0dsl3ReyEws6cQyE0s6MXta9zlOgfbEY1RiSSeOOLGkk7KHXdIZp2BoTzxGJZZ04ogTSzox2y7pvEiB9sRjlF3S2Y4AtHQ3Mtm6tsXohycuWbu2xeiHdgi9YvTDExfpNaMfptFbNZfpbbobmentmsv0Dt2NzPROzWV6l+5GZnq35jK9p+5GRnrXoblI7yq2HZnJrRbL1DbbjszUdotlavFZU2KnpDKtifWcjS062cuu52zRdpK9zuw885i5M+Y4DH1nzHHKtub4RQqsOX6BypjjNOKMOU7Z1hy/SIE1xy9QGXOcRmzN8Vjmq3YJOc/8gpnoHKehn4nOccy2LvlFCuxElQtUonMcR5zoHMds2zl+kQLbOX6BSnSOw4jPI9E5jtnWJQ9TcB62c/wClegcxxHbzvELmSM7z/yCmRitgkNPjFbBbDuE/CIFp6wHxKiSGK1CIy6J0SqYbYeQX6SgSRP/ApUYrYIjtqNVLmTO7DzzC+ZKFAZo6DtRGKDsUxYG4hTQ1Rft/v0u2hua/JPgFLswuv12VDuE/CIFXdYYLlAjURigEc9EYYCy7YyVixRsWRi4QJ3ZeeYx81Vbw3e//fKvd99HpYbyB2gA2+dsvnO8I27VXLIg72y+c5zp7ZrL9PrOcaZ3ai7T6zvHmd6tuUyv7xxHevuhuUhv953jTG/VXKZXt44zud1imVrdOs7UTotlam3vOBO7JZVpxefMJJZv1jB5FcMhXmoDbH3KOaotOkQ7T07RLvHitVOZPVEgoOxhXf04BdPWGmLUShQIaMQ7USCgbDuIPE7BPGyBIEaVRIEARoyHQ5R7mS1h5lOZPWHmU/awDnycgmnrAjFqJcx8GvFOmPmUfVozP0zBOqyZH6NKwsyHEYt1GNV+OlazZn6cgm7N/Bg1EmY+jXhaMz+WuRLGO5W5E8Y7ZWu3PEzBPqyHH6NKwniHEYt1GM1+OrYdRH6Rgm6N9xg1EsY7jXha4z2WmTHJqcyMSU7ZdhB5nILzsH57jMqY5DDiM2OSU7Y2yeMUaJM8RmVMchpxxiSn7GWd7TgF2/rtMco3kYNVafU4fBM52JX2ieubyJle30TO9PomcqbXN5Ezvb6JnOn1TeRMr28iZ3p9EznT65vIkd7im8iR3qKbyJlc3UTO1OomcqZWN5EztbaJnIm1TeRMKx8XZrRuSWVaEyPIG9pMUo9qR5C3YJ3IJ1RiBDmWmRhBjtm6ozxOgR1BfoFKjCDHESdGkGP2st5znAK7mvMClRhBTiNudgR5LLNlGsmpzEwjOWXbEeQXKbAjyC9QmUZyGnGmkZyydSN5nALdSB6jMo3kMOKeaSSn7GIN4zAF3a7mvEBlGslpxLqRPJaZGEGOZSZGkGO2HbdykQI7gvwClRhBTiMeiRHkmG3HrcQpGLp/PEYlRpDjiO0I8guZiRHkWGZiBDlm23ErFymwI8gvUIkR5DTimRhBjtl23EqcgmlHkF+gEiPIccSJEeSYPaxhHKfArua8QC3d77uJq/Cqz+GySftt/UNhL19T12Pqqbt9kdp1ULVFqBXDH+ph1Fao9rNhxNU23enL1Haqthm1Q/f5MrUTqj2N2GW7fJlWesbMEVun7fFFWjc9YeaA7SJbfJlUeLzMP9fdZIMvUwqPlnkNbHywzD/VDY9VUY9/WR94RZ/BnRk0vtmHf+eHquxIL+2MeDFtw9DPjAUOQz+rtaljmS3hplOZ3fq/sczMDBUqc1pvOZaZ6RKnMrf1lmOZGQucySxHfqhKdCwLHgDR70IvR03Y6jR0bX3HMjPd4VTmsEZwLHMmbHUqU1vfscxMdziVeVpPOZRZDuspx6iScNFhxKUm3H/KtpPGL1LQE7Y6lZkfqhK+5EpmqArVqz3wOK3aA49RZ8L1hxHXzFAVys4MVaFsbYqH6a16qEqMygxVoRHroSqxzPxQlfBY1ky/OA090y9O2XqoSpjWpoeqxKhMvziMuGX6xSlb94vHKdD94jEq0y9OI870i1O27hePU6D7xWNUfqhK+Pbo0J8bj73E+hiK/bnx2Exqj7Ev5+cz7VMmv33/4e2v73/48O1Db/35n/r556e+HvOb4w/L745fLH8o/otdQvnT8ZvlL8XXj3crvH66p8uOxL/qmQD4aunF0KelV++y9oO9qkezZvAZvQszQyOwzOHdVszWUyTiFCxr3MaoxNAIHPHpbUzK9lMkwhTQRooXRzhGVe+I4oibNW5jmQlbEMsc3hnF7Gmd0TgFy3rBMSphC+KIT++MUjaeIjFuU7CK9YJjVGJoBI64ecsRs7t1XeMUDOsFx6jp3Usc8bImaywzMTQCyzy9IUrZeIrE/Tt5F+utxqjE0AgccfOGKGZ3a1rGKRjWtIxR05uWOOJlTctYZsIExDJPb15Stp8iEabgLNZgjFEJExBH3Lx5idndGoxxCoY1GGNUwgTEES9vXmK2HrUcp+C0BmOEqmJwxJfG1V6BH1jF4IgvAwggt9rWVchtdgAB5HbbvAq5ww4ggNwp+1chdskBBBC7ZQcrxJ5yAAHD8qER5onxkRFKa3VdrJDa3AACSO2ujxVS8QlTB4zPi1DvAz4wQr2++MQI9bYt+ICpj0PFB0x9yyo/YeaRVXzEqnlkFZ+xah5ZxYesqkeGT1lTjwyfsqYeGT5lTT0yfMqaemT4lDXzyBqfYG4eGV/L0c0j41s5unlkfClHN4+M7+To6pHhUzbUI/tTdTgqHj7fcvjcnfA1eD4Gv5yzz3I/vP314z9/jsV2JHYzsaNciP3vb968//jup0+Mf/z427uff3n/4fOfXf9698uvf/wHeq9jjT7r+v33/w8Nv8uL
We are proud. What are your thoughts?