This is the scenario in which I noticed the problem: Two sets of 4 lane inputs (call them IA and IB) go into an 8 belt balancer that outputs two sets of 4 lane outputs (OA and OB). IA is supplied 4 fully compressed belts of iron, IB is supplied nothing (future-proof input for next train station perhaps). OA is using as much iron as it can get and OB is unused and backed up.
I would expect that since I am giving the balancer 4 compressed belts (IA) and using only 4 belts worth (OA), that I would get 4 compressed belts out, but instead I only get 2 belts worth of throughput balanced among the 4 belts.
Here's a well known 8 balancer showing the issue: Should be fairly obvious to see why - going into the final splitters there are only 2 belts worth of materials coming in.
These are at least most of the balancers I found, all of which suffer from this:
I made this sort of monstrosity (actually not that large, 12x12, but I'm sure smart people on this forum can figure out something better): but it is not universally non-throughput-limited. It is only non-throughput limited in those "4 input" chunks. e.g. You can put 4 full belts into the left and pull 4 full belts out the left, or pull 4 full belts out the right, but if you were to put in 2 full belts on input belt 1 and 2 you would only get one belt's worth if you tried to pull out of output 1 and 2 (you could pull 2 belts worth out of input 1 and 3, or 1 and 5, or 4 and 7, etc. but not 1 and 2). If I expanded this balancer with a small shuffle (swap outputs 1 and 3 and shift output 6 so that it becomes output 8), the balancer would be guaranteed to be non-throughput-limited in every case where your input and output belts matched, so you could put 3 belts worth into inputs 1, 3, 4 and then be guaranteed that you can pull 3 belts out of outputs 1, 3, 4. It would be non-throughput-limited in many other cases as well, but not all.
Is anybody up for a challenge of making a non-throughput-limited balancer for all cases? I was unable to make a reasonable sized one. Or a more compact version of mine (non-throughput-limited in chunks of 4)?
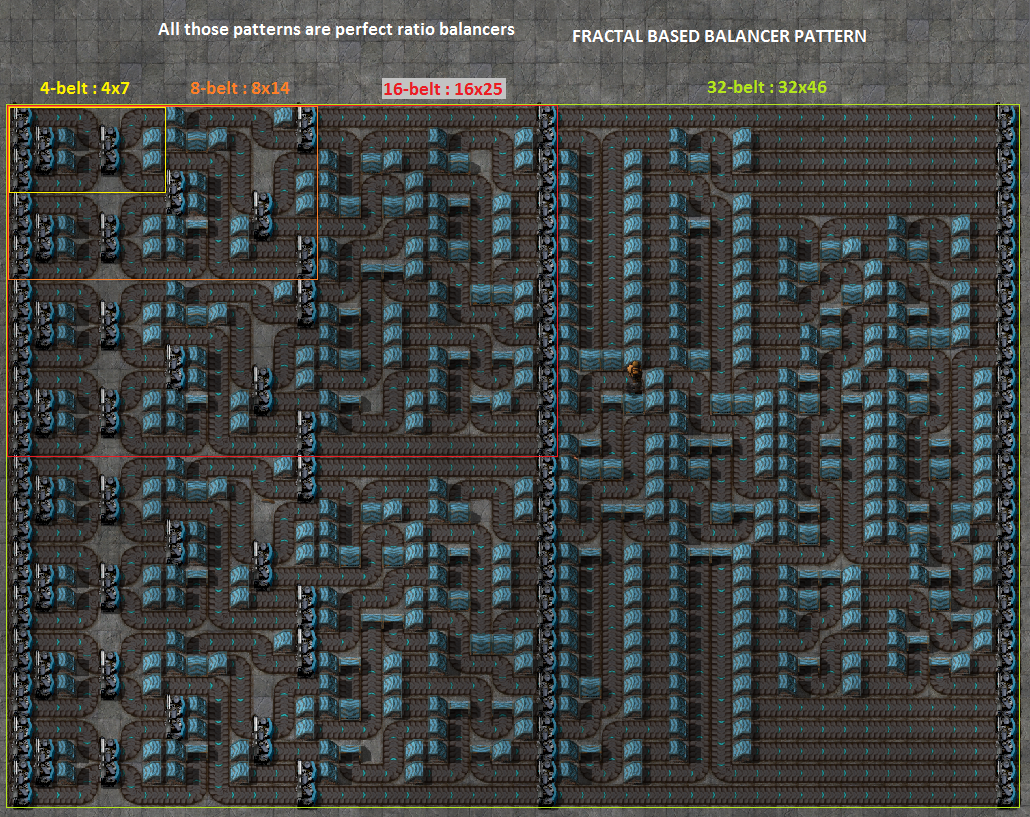
BTW, the "standard" 4 belt balancer (the one in the middle of this image) is non-throughput-limited, but only if you include the last set of splitters. Sometimes that last row is omitted because the outputs are already even at that point, but that is not perfectly non-throughput-limited - if you put two full belts into inputs 1 and 2 you would only be able to get 1 belts worth out of outputs 2 and 3. The other two balancers in that image are throughput limited (inputs 1 and 2 to outputs 1 and 2).