124776
Based on the wiki article about multiplier : https://wiki.factorio.com/Tutorial:Comb ... s.2FArrays
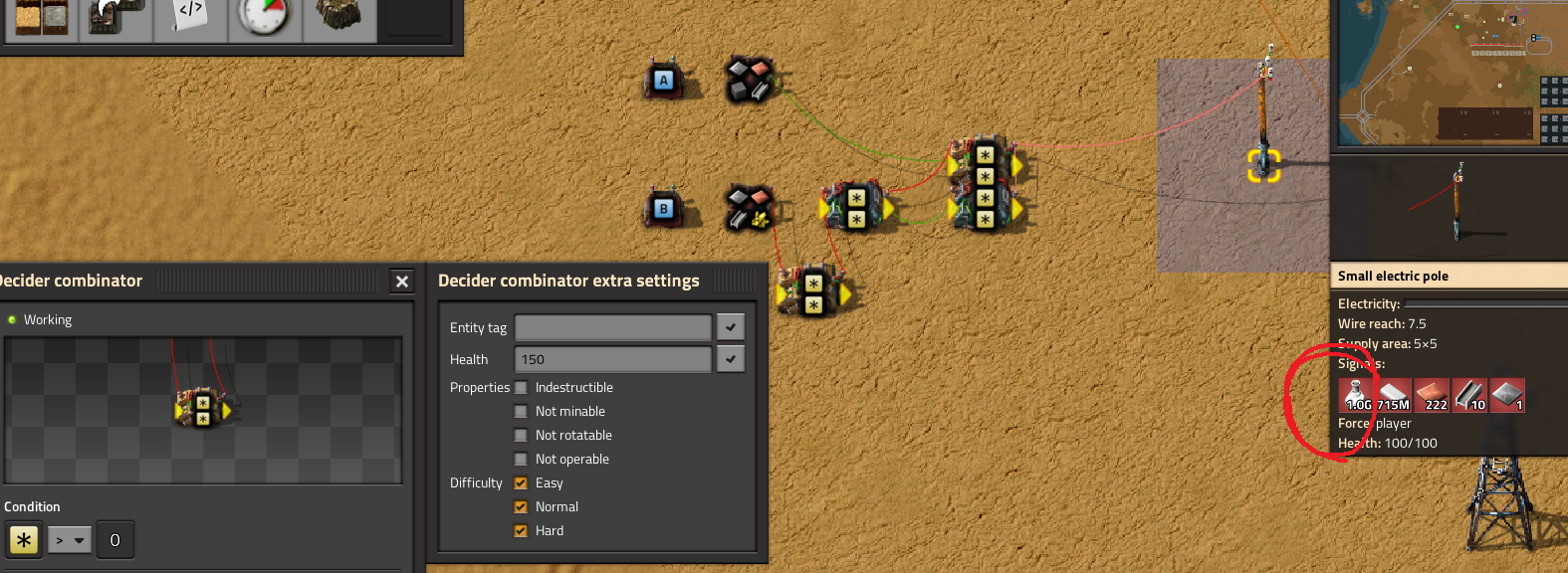
I have looked at this circuit to try and understand it and i think it can be made with less combinators but maybe i'm missing something.
The original contraption doesn't seem to properly restitute the value of a filtered signal when its value is around 2147483647 in instead show -1 , -2, and my version does the same have i done mistake somewhere ?
The math it does is : -1/2 [a²+b² -[a+b]²]
the red wire is used to make a+b before squaring them in the combinator the result is turned negative and summed with the other 2 combinators that does a² and b² this sum is then divided by -2.
It comes from the identity (a+b)²=a²+2ab+b² which is turned into 2ab= (a+b)²-a²-b² or ab=[(a+b)²-a²-b²]/2 or again ab= -1/2 * [a²+b² -[a+b]²] if you mutiply both numerator and denominator by -1.
Code: Select all
(a+b)² = a²+2ab+b²
2ab = (a+b)²-a²-b²
ab = [(a+b)²-a²-b²]/2
ab = -1/2 * [a²+b² -[a+b]²]What is the purpose
i'm not quite sure yet, i've read that some user consider it very useful to filter signal for example, one constant holds the value iron=4 copper=9 coal=12 green circuit=8, and the other constant, you input only coal =1 and iron=1, and the resulting operation will be a filtering of only the value coal=12 and iron=4 at the end.You can also use it to multiply a and b