- First, your factory will obviously consume less resources, thus reducing the amount of time needed to maintain mining sites and increasing the period between the construction of new mining sites. If your resources settings implies scarce resources, it might be crucial.
- The second advantage, is that you'll need less intermediate products. This implies that the logistic in your factory will be a bit easier. For instance, the advanced circuit assembling machine has a slow output but a fast input. If you use a blue fast belt to convoy the output, you'll need several fast belts to provide the input. With productivity modules, if you manage to keep the same output, you would need much less inputs. Thus, it requires a bit less belts to convoy the building materials without having a congestion somewhere. If you use robots though, you'll need also much less robots to feed your assembling machine.
This is when beacons starts to be interesting. It is not possible to use productivity modules in beacons. But it is possible to use speed modules. A beacon is usually not very effective due to it's very high energy consumption. But compared to the 882W, the 480W of power input for beacon is not prohibitive. Using two speed module 3 in a beacon will give a 50% speed bonus to any assembling machine in the range of the beacon. For our assembling machine, the base speed goes form 40% to 90%, thus almost doubling the production. The total energy consumption increases to 1509W, that is, much less than the double. This advantages come from the fact that, the slower your factory is and the more power consuming it is, the better speed modules are. The advantage can grow much higher if you use multiple beacons on multiple assembling machines. This is what I want to calculate.
Optimizing the energy consumption with productivity modules and basic beacons.
Let's say the power efficiency of an assembling module is the energy cost needed to build one item of building time 1. If some assembling machine/furnace/mining dirll, requires a power P and craft/mine/smelt at a speed S, it's power efficiency is
power efficiency = P / S (in watts per production units)
Now, let's say this production unit is influenced a number a of speed modules, b of efficiency modules, and c of productivity modules and let's note p and s their base power consumption and speed.
P = p * (1.0 + 0.7*a - 0.5*b + 0.8*c)
S = s * (1.0 + 0.5*a - 0.15*c) * (1.0 + 0.10*c)
For us, c is given by the type of production unit we use. (4 for assembling machines, 3 for drills, 2 for furnace, etc.) We won't use any efficiency modules, so b=0. The number of speed modules will be defined by the number of influencing beacons n, every of each is covering m distinct production units. Each beacon costs a power p'. This cost can be amortized on the cost of every production unit, by a factor n/m.
P = p * (1 + 0.7*n - 0.8*c) + (n/m) * p'
S = s * (1 + 0.5*n - 0.15*c) * (1.0 + 0.10*c)
Thus, we can estimate the power efficiency this way :
power efficiency = [p * (1 + 0.7*n + 0.8*c)+ (n/m) * p'] / [s * (1 + 0.5*n - 0.15*c) * (1.0 + 0.10*c)]
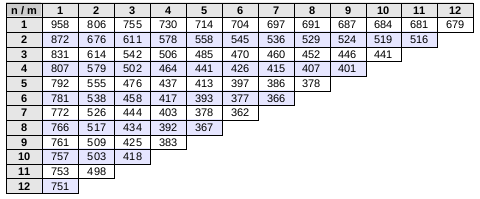
We can use this formula to calculate the power efficiency in some relevant case. For instance, for assembling module 3 :
p = 210W, p' = 480W, c = 4 productivity modules, s = 1.25
and for electric furnaces :
p = 180W, p' = 480W, c = 2 productivity modules, s = 2.0
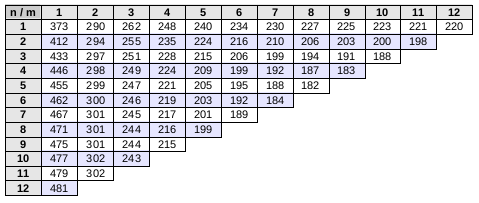
I've done the assumption that n + m <= 13 as i don't believe it's possible to cheat this law. n increases downside, and m increases right.
From this numbers, you can try different patterns for your factory. I personally use very often a very simple pattern with rows of beacons and rows of production units, with usually something like n=4 and m=4 or even n=4 and m=8. I'll show some examples of this later.
We can see that it is really interesting to increase the number of beacons in these two cases. One beacon for 12 assembling machines/furnace is possible, but it's more complicated and not optimal when we use productivity modules. The inverse, 12 beacon for 1 assembling machine is possible, and not that bad, though far from optimal.