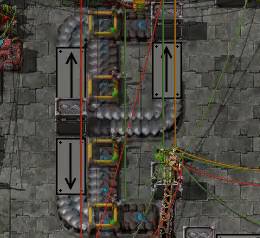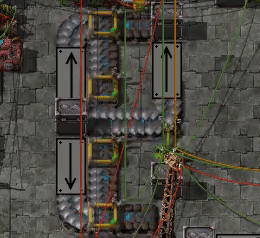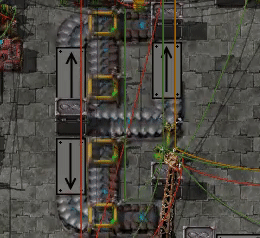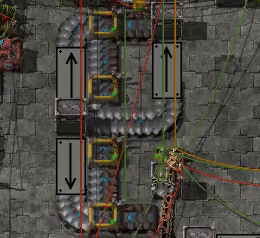
The wiki page (as of the time of this posting) tells us that straight segments have 32 "slots", which are travelled 1 slot per tick on a yellow belt, hence it takes 32 ticks from one end to the other. (The page also tells us items take up 9 slots, which is no longer accurate in 0.17, but this is not about that bit of stale info.)
The length of a straight is correct. But then the page describes turns, and says the outer lane of a turn is 37 slots and the inner lane is alternating between 13 and 14 slots, and I couldn't get it to work like that: I did some spirals with turns in only one direction, and cancelling out the straights I got that the successive inner turns took:
13, 13, 13, 14, 13, 13, 13, 14, 13, 13, 13, ...
I.e. only every 4th turn takes 14 ticks, or, put differently, an inner turn seems to be 13.25 slots long. Outer turns too don't quite take 37 ticks each:
36, 37, 37, 37, 37, 37, 37, 37, 36, 37, 37, ...
First I thought that was some off-by-one problem in my test rigs, but it's perfectly repeatable.
Now I got intrigued, so I set up circular belts of different sorts where single items go round and round. Then I added some circuitry to predict the lap times - when the constants are right it should line up perfectly with the real measurements regardless how many laps it takes for the cycle to repeat.

With some deductions from the lap times of those circuits we can measure the fractional slots for each type of belt segment, also including sideloaded belts, underground belts, splitters, etc. I included some sanity checks too, like checking that left and right turns take the same time.
Rather than dealing with fractional "slots" we can scale things up to whole numbers, and so we find that there are in fact 8 times more positions:
- Straight segments have 256 positions per lane.
- Yellow belts move items at 8 positions per tick, red 2*8=16, and blue 3*8=24 positions/tick.
- Underground segments and splitters also have 256 positions per lane.
- The outer lanes in turns have 295 positions.
- The inner lanes in turns have 106 positions.
- Straights and underground entrances sideloaded "early" have 188 positions.
- Straights and underground exits sideloaded "late" have 68 positions.
An observation is that it's possible to get items to travel faster by converting inner turns to sideloaded segments. However it doesn't affect the throughput, i.e. items per second.
Based on these findings I'm going to update the wiki page, and also fix the stale item size info at the same time. But I thought to post here first in case there are thoughts on this.
If you want to try it out yourself I've attached the blueprint below. It requires that the infinity chest is unlocked, which you can do with the Creative Items mod, but other than that it should work on vanilla. The test is enabled by turning on the constant combinator in the top left corner. Because I'm a bit lazy with the combinator logic, the speakers will alert when the test is turned on or off, but once that has died down after the start there should be no more alerts as long as it's kept running.
0eNrtXdtuXMtx/RWDQF4S0uj7xYj94vjBBoxjwMiTYBCUOEcamDdwRidWAn1A/iIv+bF8SfbcyNH0pWo1R+Js7vaDbZFS7727uqrWqq7Lf529v/k8e3ic3y3PfvNfZ/MP93eLs9+8+6+zxfzj3dXN6mfLLw+zs9+czZez27Pzs7ur29Wfrmcf5tezx4sP97fv53dXy/vHs6/nZ/O769k/zn4jv56TC1w9zpefbmfL+Yf8Gurr387PZnfL+XI+27zR+g9fLu8+376fPQ4PeVpq9c7Lq7vl/kLnZw/3i+Hf3t+t3mBY78K487Mvw/9KMzzkev44+7D5rTlfLbB8vL+5fD/7dPXLfPjXwz/5eX6znD0W9uKX+ePy8/CTp1fY/I2LP6w+4MP959Vmyr3tGD5lvrhcPe3nq5vFbP2X7u42b7BYrStX//XxcTa72//U+fXwj6X4+revX1c7erABqiaMzPfH7ffLX1vWDmxXvRx+dz1/etOf54+L5SW6IxsBnf1GrP5w+3D1uH7J35z9bvgH95+XD5+BJf9ts+TDl8v1Tl/+/Hh/ezm/G9Y4+83y8fPsa2F7H2fXh5s7bOGH+eOHz/Pl5o97u7z6s10JLisV8+0/HCQ8PFTxniKLq0qpCrLW6GEPO2F/v8P++9Jh5++/FOFQAvnvN+BZ9yd41n9bOevf2sb54/3dxcPN1XJ2vKNePsvJ8TzPGKDy6WbL0LaeYfXyM1zf3/URvpBi9x/CkRGG6UAhFKIQpi6L1JJkd9oRXjaz1/bXNr/bKr/bzwu/TGf+uNqzxWy1xuU3qnP/MBsUZ/0KZ//S4CX+dPYV0A6fHuHtic+qTODJwb9EDvKHyuGnPTmw/9FfVv9oX1D/1CCoP0KCklIWRZX5666uT0w5BtD7mNfwPn9skeCfNiZrz0v9a4MI/1pxUxvA+xJNLLgth6lsGVtF1C/J6fmlQ61LQILhaZIUrZt94kBWRh4IkhK0JaqzNuowHtK2WCZYEG9LD31xXVUi6VLBGECHaWMxqUHLbpm2R79EFB2O5VXEI3BMUlyTK0o0HiB6POBAFBUjSfl6GQizyfWFFpOi9h1XN+PqjFUtOjPQ/padnwMFbDvYSXbX1cGO9GVBRgjtOD7a8SWBexDeazNBLkUEJXJiy252aN3sE+dSyjD9RwTNi+4o4HCvK9aDOqaKgAFcMSqB43I5bYqkJOaiFfPiQMmXiKJTpLweOIQirbShegXEFSWYHqBFB9fN4Dqjj6XLVoGC6xLWUmhOgPLTw1qKulBl3gApMOCgQmcylCwOmYzSZa0JUL6NYTMZHUoCt63adeLgWnNRGZ5EoEyHAsTmawgKeMJ4MYmi8i8R5TQBNni7zBYFmEqgXKesh1tdcROEt5fa1ikr2ziCkQelO7huB9eODa7BNK6y+9cCFLDseO9wd7Wo4z1dxmVaIXhPCzbeM6YkcLScQInpsSlNxCY0MzahwdiEjN0LHoqiojyCytUiLumN4HlBrVt15sQ5EnsDDAyspZ82sNYWc9HaMU2KfYkoOl3N6wFEVzWBvtmiBLMGpOvguhlcZ/Sx5FYMCK7LWAvNEpB6glgr1LXJSKY2gREHaTqToWSRMJnyLXpOTBUTGthMxha1K7Zq16mjMmZaocHzCaSYNiozYMrfITAoGR8DVjtI1YneoUko2xbKRUhLZPyxNUq9RKM6uM5uvhUIuDYEqWdrpMY0MnZs3YytM1a1hBLQrJCi9zdgooLvaC8RBpGnYCptQRyC9gw/T8GVUuwNmqfgJthUgQhMGGZgwoCBCdvBzKEkKqpD3d3aWAcz1jHBjG/UmBOnR+zvD3iO78TZUcS8sxVMexJfIImOqvNaECBUTTAoriQtmi7QUXU7qo5sVB1AVF1EWRbMDphghxCrCVVigiyr2rb6xL2z88wmaRg/F52+UQcxaepYplkWom/piS/Tt1KemYUzCDoCoDTNIgjAWsJseabZsu2CnCSotuB1MlsQGEnvFw7JRlfsI+HjpXNEiwGuF/SQEG2H081wOqOHJelbFE4XvR6Wk9Bj1KnUiIwEV1FiqCuI5Wck+NKdhMWqJXqyb9LqsiJN6g7YEyUvXvFMsgM7N46kATn782Xb508pAkAF05g1cg7ONph6+o4DOyY6ZrdWp18giU5P8wYH6gbiiIaJbEliaQGyB6jbEbVjd9pzaKe9IsRyYBqAtONwz0Ez3TPG+nuSc+bYEo0GXTkR0QuEUjh+o8HgSvL2jed9QnjMEQ3cPPNy08EJA1MvcnNgwoBn1nK4+AJJdDyW9zAKwmMEx+FK0mMJA7K3AUkkUXZHlOGTgciL56IOj5U3yJ5M/QJUzU77cGjaRxFleKxPQW8CkhnnQ4xYXDGaEqq0CKr0/CmLsajPYEMDpUbCopgT+rxp/P4JoWpPRGQ8c4SFx4YfqN67OpFExXRQc0YihQC4GgN3SexNEilrFaHCOE80SfTcWY3+BZKc5sxMsEciWxJYdoDq7T9eMG2R3VvPo731yigLbFCg4vRQRiBmMAVmuW8QjXt94og2MivXA8bQe9tu+igmDK48SSx3SsuePLDHLSpRlDecOzD1USIBzMMNTH4TsEIG3Sf0JR63oljUiL7o6/yGbT/NC/Sp85v83kMlioGgsmx9xOINunesbkfVgZ1THcAMkIrnwzIg+qjFjNiIDIhQvnIK0ICS4PhIpzT+J4AZEHqCjT8CcREYmBGJgEUktO9Y5lASFdUhhKREIAamMYc2hNioMafNhdnfH+G+iFOfRB/BMYuR2f8+yhdIoqPqvBZAedWRaKfHliSWIWD6kMV2VB3ZQxajQFF1CWVFLIphVEfViTCIfgyx3BMsQqg6svsxKFnK+IlgBoQZR+9kJbkYwTZ+/4RYRSSq4COTVUQ4d8DYieMx8A4yMisOo3+BJDoey1scaHZIJEggW5IYUzemM/VDSVTcMWH4lKzXmvO9ENYwwPiOqttRtWejanQmahFlSYGVP5jYYXVyjSSI8YpSlEUpBTSWJHlWBVorUxQ6lothZbfNiRxqIiVCGmo1OLdmnZXkWefhLTCSYCc4KjOjYeekThW2Wzdu94lzUv55g5MQrJo2UZIC7dUlHPc02hcIo3OlvCZANahSUK3y+cLEkgas6UC7GWjndLLoy8GkvBrqgmMbFzu4HZlSJvT1GzuIyvEPh+p40SDGP5TVMb//UtSh0ookF7YbHLe4466bvX6xDtXh0TGpzO+PCWsDRWUigW2jIUwmUbevD0fC8FU1Eu8uJdcYR/DohBM/Oj+CEFG7LwJGdCO7ilgwSwQHY/K0B7ez6/nn24vZzfBtj4MZfri/meUku808iZDRqh/hFCQQhXNShkMt0+LwGaL81RL3O89BdfFDgeLvWxDGnw890z83WNGfUM9EmkpZZ/mk0HVRoM+sf3F7dXNDn2LbcIqJdgHk15usZ8h/EMirL55uCw5Opzsisf7zHrEOjeGLn74JhuzFL5BF/rK3iFHmaRUNrbIfJ3hew0GRFMnO++D7WvkcUnh4vP/4eHV7e/X+ZnaxeJhd/X1WE34s+NrdY58MUaOrRc3QXxOi83///T/rn21faPWLwUauT+JOcpe/XN18nl3OF5cP8+WHT1sys5LPYvDAt8Nurbdv5bjul7PN/wcR9NoxDNv4zdOHr/zy/urD3y9/ub/5vPqK4QlPP/t4c/9+sCtfnt5m+MP9f1wO1uXLw6f7u93Pv65+MXtMPuzT8HfXv9igiPPNT+7vLm+vHnY/2vzD29licfVxtYf/fjf7x8PwQbPrX72f3Sx/tZzfzu8+nuWPjAXhmezwTFrKXkPNyJP1KvBMRi48czhQUZMnyPWcbC1EcbvxeMRe8mvHhezjfqBpiggqUqM9VFmBAspvdGzhNxShkSL5CdUITqUUp4x/UXouemSHPpaSmL+khSZcAhEakoaKEFR8COm+mEOJpBIgedKhRUWIUn3ye1R++/OfJFEIvauL6hCaJUwl3hqEVmDiwNOJ6Yz7xzJuz2fcbAuocdxnpw6zFQGzZRFmK2zgw8Wu3n/SaEVRWEGRaIWYtqQoEBuSTh5sVVSkd+emBSgw1KFND3XQu2+gUIfihzoUM616fQBQGyw79yatNGU2NJFOQKUK6rKZ9yivkC28gmiMoRR19mPWUOY/CQ8nqJZvonij0uj9qNQ2CSf44mdGmD6JTp8QrfRvjT5pgdInMVH6FFe9O16NPinHx2xcSKbxdAoVpk6ftCXoUzE3QGN9HS6U7whYUyhAYwhY8yc6aC4C1ngUYq/Nd0fA7P0/FH19MLyiLmp0sZRQg4GOXbvwSQc6aHkRXSc1Ueqb0fUDZJxA5cB2mrSh0VyvalGuoVqS2tbeu7obAb2olCYhYaZs9RwIHJ+mjUwNOA6kTrwictSarwTsM+5RormTfieaPOUOb45oBjCqpEyTVfRJsi4RZyLc1sYr5T8p4sBPTp0/mXrOkC7nBBmswcOFjB2VrTetimsMASO0IiiVIXoEaJ2syHZIhko+MVyPZSQI6UUn3/TuQzO6M0etLHjBJN9GoWhbtmRBUdwlDdOvvUP1n9gEsZsiIzV4jGFvTHOPMbCP2eEJr8cYtKUSBcsSNSAekr7l3BIfqB21ATbrD/KfZFFWIF1nBchxNW+NFRg0ivA0tbxHEX5oFMHwowh8TOZBQK87JjOeMthY9ZPxfEzGrX4yAQcrZuq82EqCFxfDEAYsIpGq8+LMuT+nTvshDgqEZhH4Xx/mLxl+TTJpBSy3EZwVuK6KTixIpEbVKNl6GMxQfNMWra+VMCNuyd+j4kbpZdLaL9Q/KiaMOBY/E637iFMFjm41UOTVgKMVbKvGN1oaJZqx80wEi7w5nmnhaItoibYQrWSMpryCzqKM/CfBTTMv/ORBdqyD7HJKkMW6Wl7YjrHXe1Y/7p66OiIKtS2R42UOb4MNP43Wkhg7cN0VGOdwPcxBb76DwhyWH+awjhnmsHiYQ3fmRJpoymi4uqgp2r3593mBRripYkuKiiUujYxDLw6lc0kqZDEN3cFtIxo+0hL3ToZKFnUq6wvyXyTRVMRewvIaTJCfjct2rU7BiYidCSJFmm+uX4jDpm/2hnvrHavbag9hMceeqZmsXMRiDh7nIabOhR2R2lJOXXFw5KHjXlocFONx9diFpbqAuGIo3TkQ9zYhQocG/9dKXf0nPin4scXaeIeR8H5HmjPU59iZ1YYYoeCIABBFBm0FQ9Juy3JBJli60MIKLfG2ZEDEi+zm5z8ogtO/Jptz9apXZ44/3Id9lr0ACZPtfAnx4m+ubsvDTSImf8vkiRYR5dwNj7WI6AVOmy2rO0YCxWhDJHJ5IhfHHXpey++v5ymQ4rnNXDwW1+hznhh7r6C4hufHNbxixjU8mLfQlMrliGC8pSbkeJ/VqfwXoe0RmjIx1m6rzl0cobVpG82kXsuV5QZ3RexZlQyhkra+bspJQuvLxxbteCD7RQMk2jeXcuYDRrLlVG8lpTHhFVm256cE8cEYVpIhbUdjnsqYDxpDY/ypm0Ez0ViAiyV6XVMg6pps8VoioIUMTRXSa6HWQIEX6C2EjClSLFZvBQWfqV7YTwuV4nahfjPhSDJQDK4HMMGg9w5kiMtTxXS2fpud8R51LT98g5UCF/0HVazluZWzwYCYcbJFTdG9ZjV84LcwCoqJGQPaPUP2oibIJbi3xjCDA4ODLZ2PHHEF76kmUcFmbXX+i+BBnr2hXqwDbOXLFidgKTF9nNNmz+rHnUIqRP1C8oQEqRBDgbyuOCOKZEduCW7AIhxK9QgHufkhQBGOAEQ4AhOARjjC0VvZM6AHZTRivc7RU7mTsVgbE9EgSlPbXU/1wQsevVyTMenk64sjq6LCkFBTx3Xq9smTUjZZX5D/Io0xQTXVvmjKv2aKXuR3t2C71mhAIqh6F0UIMKu3RgQjNltTxQ7GIjVaM2J99CJ/tGbkRgMjnETSx3NFT7DhMlLyaBVMS64VFYdO747Wx6A66EWEBCkVIywRblrQp7UyTh01ZELUp7UGarKRKENfjIhr0YM4pLgy1vwAuHuiMU0kokDhMGc48Pvr0q6LWT0/nCqMZGjdScZrkAx+4wS+6CVIMnQf4AR4BCXeGskYvgiLsTRN0A7EbVKwlKPNm+r8F8FDNbSdOL5eYc06vo7F3caGamrfgcp6z+rHnQIqod5nOHlCAlQOq/ID2xklL5e+veN6KyzAoXsHPcbmQ5OTMyetLHfm5OS1/EEDHDoZJU00ZTRknYxGarCsFEWBehAjxBaMQGSkREWd/Ji1kvkvCmhUqCXJhrrzz1yGCU1JKZ2GbIpfGUE2YERnA4hK+rfGBiQYOtgdmAmGDuQrxg4SiFWDa1w0JuGWEEZNnTcRs+11MYNDSawnhOlDstZbVkdAGPaVio19JRf7Sjj4YGzHvqSakdi3fj8YPYWqfFGgWHzDmB7fyCjWOSZPTWU/SyK+keRk8YPtDDOjuR4VbYphWhLYYoAvkiXFBZVOWIYtfiVYr2Bcy0cSpWTkVa0M2TOW/yIPomA/VRQsVrrwaihYar5Ss3U2oJzZd86MuHL35jhzhCFfnDpvUvVEC1NMjFFKQHjMis6bFFEErZSEeJMSbN6kJJM3KYmJVXaYndncc0pQhxDIEpKm2q0JnfyEPe6WcS6ZRdbrv4iZYKs66yaNNHm+iO4M1DX2ZoG8RDVInWxLXkrmNkVSLUIExZ1i2ciBbR9tS0d+KahRW4LUO5s1FPlvQvsbWNPxMqKEb62DnlIObFNvJsqudXjFuV6J8605craffg6sDBoyHKHsLK8do/YscoTYiyoJKgO9355hOqvL7CXsbcDP87vhlxcfPs0Wy8o2hK/nT3/5cjFbLgfNWmykdnv/y+zy893myM+uL1f2cPEEJDOPj8Dj3dEfrwVL/G7c4pdSJA41yfMoO1QtARmJ48tI8R+/y/M55uM154jsHjzeI5KE5HUxi0cbltaIsRvNZEh6OQikLeuU6LFvSfFWUjtAS/XxtZTlx3elAqPVUpVqacKMylmTGvD1u606powAX6+O7+uNAB5vj/94yTmhauRQQ5nk5lwW/YhRrC2xI1faREWHs1DcEs0/pPL4YMewPLuMYz+kxSifscD+h+Pvv2Ptfxj7/h8mw8jUbKhi0NJ4QEbHd2MG8KK7MTnHfHxkHRE5cqNpkyi2LeIay2LxUo1da5JyElXk7Bbg7MfHOpbl2Efu15UtAhsLeHFz/N3n0fOxG4iYGIjEh+iin7d8P398smr5XPn47stymPLI4xTp0DVlk2zLMgi0gbFFY/cmxQnmyvJ5+vEZiOP48rHzj+I8P+X4flseP9TuOH5bjjyum87RUclk1fLoXOX4vl0eP4jlDP/px7+tc5wotxz5ZWlu/qZLzkex/YjjUHg59jBfcc6Ucnx2ro4PrRzLdY/9GqbYoFo5vu9uj3Fvk3j281rShKfnETrD197eX69+PfvH1YflzZezvXyWv2U/w3NQgBo7hcmMb0s7bBZDxZ5zobAfPH+lXfndGTS8wLOTfDZacH42HNLHx/n17HJ4gQ9/H977P2ffJkE+bxk/lUAdn5d7TiaBiiMTWOQX/nsPC4wPd1Q8YXMGRBuOHzH2HESixx4wzoxxKDJcz4qBjD1/xWt2u2bl+Zca+vi803PuNLQbl2VMOidVLGNQqGUM/GwGfXwiGPhhCu1O1y4HTrxDjz3510d+g67Aj27o419/B87NhR777Xfa/aDcFi5wIi5m7DdpmRZyScSl3LgocPCNGTlZrLS7CPyIizk+qwl85GCOf9McOMjBjhzbVgr4Ih8G2OMzi8iHAfb4N5mR473t2O/pMo1vDv15pTnB3ni35ePV3eLh/nF5sSqIq5T3HLSAUNl1Db6u+2Ei+LdvRSCVSAop/3e/kHJ2t6oQvbyeL1b/uysp3P32cXZ1ffnp6u569U7LYScWh39j9/PNX92gUAHEUERgD3WSZVPAKkHY2WDHqjE/uWiT4IcHNRwe3JuDRR9ql91Hl13X4+vavIyRaj3z/IanRrwiUvanTvY7tODVD8r8WRmJzkl+hFcbUOf03nwYUjd2RXaW1jm9N0WE1jlR0TktNP6G3dUVDxN/mLQqoRotDC5cR6MavTf+gRa1/tFKPTZRK8MXtS+KGvDJ2uS1L7uux9e1nCMU8CPEWjcC66qaPZMsn6XlqHGi4sfeNXorqaXEZcHAiVoCle4qni4qkkD6uxYn/B3Pbubm/u7jxcpazq4varWKftRIT/NbpW1KGCGtAZyrch1HEaLiO1cdSs5VAs51l0lUcCoeX4llEgN+aDjuVALuVEY+gtxrBspeN7+jCnAyu4LQri4ldTHsDqHSlC5H9V5TR6Y/kH7UKEpHvj9wqD9QGj/gHOavDFCfa08Xfez1MeSeNj1q9GH4ExGsgE8b4Op2xdMcR6I8vi7H8SnA8UnVzT9xtPhRJ1s2/xEXCecIaQQzCP4R0hJfN49F9lqwLR5u5stqPbc57CGvdmby0Dhu+wU/PA4nc3jeytDNfl6eZd8AcBa2B+bq2mAdWxtcMQargRis48fltIWXZekYq7GKHjVas5bvP+F7Go3cYVZtSYAXYhk7pLnY6YI+w/cFeZCSVSoj0VU5qmo4XkF9R6dg+E5B80+S4Rs21T1N3SQ5z/c0xSiVsaiY85aH1VzLjNoFOMN3AfC1B9B364RpteH7n36ZTxw3z55XKn2RVpmICoTj8vZ6gn0eDsTjx8fhyFyXnJ54Xngroo0byrodC3hTgK6xmmbJcV/Lev4Fk0NLojTQdUueMAS0fPxRCC/nj5dFFMJDCsGPrcl+sUcVwGu2TQ2lck5tPSwRllHlp5/KE85PsJyikcKd2lgsbRB8S2tRS+v4LFUBOU5Owst2O1I8APyagmJ5kXb8LFoFRLydhpflXL47gLkDOQiOzz9VNfTlHPx+nAtP5+H3Y302nyipCMg+wstyZO/5JklL/t56vknS1SsUr+CFWJ+t4c/uJrPYyoZ9S6hE0WR6vhFCckO9hZdlnW++SdK+er75Rkg74HwH+P1Yy/KNkAaCDgEwQoFvMoOE35azCUHBb/vjwPDIbIcShm87isUOgW/NC2Ut+WNp4GU5tiPwTZLRgBLxTZJRwCZ4+G05djkE+G1ZKs83UMbwRRaRqKixSBAoSviN+71ZyZpIvjWRxSBQ5Nt3A9ChyGljWCiPHkn0REl+nDrA0ZPIT1Ddb51walG0yDf/tlMParaxZCu8Kt6k7fUvoK27zXt69WTr53dFU++R50jiOTWfwneutlrzGCO8EMMUGlb5v9XjNoX8GoCIXtkZATQQOt12Fmav2cDi9urm5mJ2M2zt4/zDxcP9zazS5UO/bIyzEyXnb4CuBVsFNTQsNUDhfXz+QnJVi65qaMBvhGvIADBfaftngNrx3bo6L6QAX9Oxvjw2XPVqzpdLAb+wZrwwUFC9i/KY7IZKBUehOMdeavj9NMN9SAO/bf4cAaW1u0iO4byfg+NOnOMJ1IrqCOxmgDeBtWyEgyecZYFC0V04gnNSFc7CWcuqhrgBy5buVQFezz4MoOHxYgAr7+d3a7CS8ZzbEyEOE4oLZGK76DOeWnwPQPWUtowSlIcvl2vccfnz4/3t5Wabdh0PuRDNpM0uDvoDrihDAbQZZRPmMTxacZ9VJiquGOc0eyWau10lpL5VWMmS+T7SSwSyAoXP0thDgF+fIOCFFLv/7EG/88xihHQ3gPJpDbXe2lapykSqGcnlt9uCOuZPT8d+W9GxukiPo2I1DSIEtUHpZZ2ymUbxBUE+O+Srx/ny0+1sOXCMuiztr21Wdwr883ndl4nzj6vNX8xWa1x+I9X7h9kg0/UrnP1Lg+H809lXQHBWpEVRO1EUpOm5WuVBrTKvoFX7YkC2+ED7/rVBUH+tqN+akr9QjEV1dJjEa34qgCJWHZwk4ggUOIllWWqJgRN2zpuTpij0iIITOUFwEghwkpNcdrv3qt+5Pk2Hafu0zO1U3adpxRWGBA2e6EjxHd+cUVrjZN3AWSmYSHGvYwNLkNp3cNIMTvi3xWtrB4GTsp/SYORE2w5OEnFQkRNtK7I0EDjR/MiJDEWhG1Douhvod4BIKSovPWGgPddAWxBl7poQTwllUuLIqmB+u/HIiZYTR5kRRZncyIkGIydadHDSDk4iH5ygkZOKnwqgedt1Tp6UeYuEect0LS1sd8Q0SoWOBSlppFgwlFUnJ6kaFmRXGrliup/Z6xXFE7rrWPAdX6SUdjql6lhQGSYW3GvPxQUnykwbnCj0WsdwQ2AGjJwo3cFJMzhR/GsdAwY9a4YTjJwo2b1lIg4qcmIqNNtgkRPDj5yoYkKsASMnMnZv+Q4QKRU5UaHuLTU3tG3QyIkS06MWlDiyKpjfbjxyIv20wYnWKDjhRk4MGDmRroOTZnCiNR+coJGTip8Cc06k6eAkEQeVc2Iql7QWyzkx/JwTXUakaM7JbtTHpHwalXNiuTknFs85kWLiPg29DbBcwm3BnBOpOjB/xzdnlNY4TYSxdGACcwtGTmLHJu3YhH+rY9GUk7KbsmDgxHdokkiDipvYSqWBxWp1LD9uoos50Bat1XHTQyaWYtuWW6pjwVId233hO0B/qCCVJoJUhnulYxvyTaYNMFEKbSw3aGLBoInquKQZl2SkWFRGNGZS8VFgtskECzYslWvi2OQZyzURHQNSskgxYCUtwWHhKcvPNCkOPjYOjpdM3JkdBj9IZ+a40RKHRUt6rCRRiIpuUUbSGSJWYrn40GGxEtshSTMkyehi0baioZKKycRCJT1SkgqDipS4CtNzWKTE8SMlppjz7MBIyQR7mjgqUOK4gRKHBUp6Mk8iipr2UHESQ5RBWe6dgYPjJFO/iHNo8bfjxkkcFieRPU7SDkocv2TYoXGSiodC4yR2gi6KCpR4zdUnLFDSE3loYaQYsMLmcoKqYUB+pMQWYb/HG6QqRv9FD1eITD0HE7WaxnMTYoFJXrveuiq/EEYRZS/fSlS2FielYjmW6LXiuBjWY5UFsue9vAA38e+XPFowVLHqGNns9UKpqnpLeHLvK6J0kCf3lu/Ji1h5bzIeS+a90UoihppELWWdiZ6pOe3Oy9FjnGc3cHZKnCfVr3NSowq7HVCgOvVKZo9WMvvIlQXGP1WvFWrHJZ5fyOwDikuKPipgHSB614/U9AVB4JJQRg8mKAiXBMHGJc4WZS5Bfxan58/SjT6nBZffbeyeXvd+qIksavpDyMk5It8icIvG9ybrcjOYJt7+LaD3TIEbQAtYvET3BivtuCTw75kCWLVe81FYvKR3ps2YTSpeElxFlB7DJfx4iYtFmTsMl+gJ1gkFS+ES7l19wO7qdZ/ok8iipj9UdMoLApc4Li6B4yVTH34QAopLuPGSgMVLTO9K+wJcEvi4BI2XlH1UFJiPMhPsshEl4aMilztHrFShD0+ihZGgwCjKihOx6FRkj6B3vliJF7F4iTEdl7wDJCopXGLruCRaJi6JcLxk6oMGI5pwFLnxkojFS0wf5dOOSyI/vySi8ZKK1cTiJX0GcsZsUvGSWOF7EYuXRH68xJexKBgvsRPsYhqpeEnkxksiFi+xsuOSd4D+UPGSQMRLYuTiEjheYtWkcYkTaCl65MZLIhYvsX3+cTMuyUmxqIxovKToo6zA+2RusYlkCpnQtm8UBxXj2p7ua9tFgxT/UNa2wjTpeuKiC7642xIdPLzJ5xEvRwSlr/991olLxImzp9tbAfaP3H7+5qi92ILUXWgL7P3+TtmmZuG8vvlEzYNQXGQLiBVsGrnlrycrVkJXjiNXTclVUYjLEJKmKvGVpV6hdjjIc8kMfqz/IuqCdpGoHwv4ft8CNf586KP+ueHk/QT6KMbxIrLvBQH4NwvkBWrbBSp+qEB/ahHoXw4F+k8NAv0jFnoUpoj4shPKqWx/5bnK6VDEYnKK6Y6IWP68j1hcY+zip28iIXvBC2SRv+wtYlaz4LaraGiVfQT2vIbDEJjhkgfALoNNNY3sYM0TVlcKDKx5NliTggvW0LmtW7meOAfhf3/EvZOaOOOVkmC8xfiCBCeYblNuJk0NpKCwmyeoQdTEDHuqekJL6hVCxcOQVpCZX2IlPjb1KXmuI8m86BWEJDV5UtiyVO2y7DSP7fUPVY2yBES+yWaBvEA1CCS2KcqdGvxQaiDZ9wqAXcZDNtsKkAljqHpDRS9EcbfBiSHaTJ6ISSq0KaF8kGS9GhHzTCIi0dDKVq6nTsTY3w/GF7ZVgtOmBiS0pvI0ItHXVXoK8BnqFVxFOUi9DFwXFHAXJDucJOAkdbwUkeUjiZZsmwXyAo3tAu1cLy+NgHE9UvUdUzmVQF2bmCY1iNq9JjUIfGrAtcsKnPWq/OTBqqKCbcpAYFWxy3ySlYtgTSlQo7dyPXGwyv9+uFrmQoWJM16lCMZbDC0pAxoR16mBoiJ5igDuXhClZakZOsAHhopGqoqHoa0gG33g+SdPLQo7ksyL3kFI0lAVxoYbaVSuXZad5rG9/qGqEUECRSWHqWIKtPIokNDTpAZSBvGK3ECxyyQBw4zHbJScOoiqz6v2srzbEQRRojMxYhiJ1Vj+lmIPHElWLjIRDWbUyNixsSaBKRG39JJoU0nmSRjK5+oaTSfPJRdPabQCaWsVTpzH87UHz0J5mrPT8STbdh0eT6JURROlKpsF8gLV7QLtZC8vDSxFzFDFBoZbbKDB8aoX24FJnRv8WG6g+SlFfMdkUdnrUTimwHVMDoR1evJoXTvK7QQIrWeuN4vHmi1Wj7snM3HKq4l7A1kGAwFUItW5kXYU9grEvYEMhF4FAiBYKvSvbUUVKStgBNcF4RkoT6OqO5TMit4ICEpaikVbLpwwol2Wneexvd6hqlEelkoPM2WBooGLOFFq4FYNWl+NGmQUvmS42XbZ4DEbP3UIRdwaKFvcbLCXi5s8DTFUqw2DpW8ZzaYhhpu+ZMCEGttxMRmwN0TQ0hP5T5lzcYh2qGx5U8HF9LHkhuUMGppxY4jM8HUHT0HRnRVUt95jrIAKMFv2SfbNouykgO2DDu0MER6g7g82C+TlifYyUb3M4BU4gedzArYmR0zyo+hhY7kuyWI5IL0xk6VuqC2G0S17zi8gVLjZiZg4yzXERYEuFhhYOKTQIV1dwTQE6RwV6HXcQK/VrZLsiI5tsQ6NJVEoYonWtZsF8uLEAhX9/s5SdyakOL2mnB0Vp3DU/Z2JFf9IumbNNQVgnMJONXnoVW8IMp6ieDTYkodDNFO/IDBENyJd7O5swQKeUUwwsNx8HotlmPTc+8zWHtp3KvdeU3CDyi9xVBzd+ooRonLvHfce02IFOX32Bbn1Fkvws/xyHLZBcHCiSc8zIQkIZTIccbPmqFp4V5anbJZnDw3khYHlgDnqtsdxY8QO7FkiJ3o7IM3qHuXVCIHjpwyxXa0De9NKOwaU6thOCe7POvmkc1vHDt4UQ1YOa88q7eRxHYnHHYbrHL87K1+F4JBCLyskpI5lfXiqh4znDrJxvlmUHaKz9ehQhSOhs1TWhyvOFHFYDEb25mAMcREdfTyV2u+oIIyn8hGdrpht0mOwSQGaODLVOoLoXrPE2PFzhtii93CoZvLdh2x9SqS3xXbOHusDq3pzd+upa1SvKCNN9G2jMRVVTOkrRtpTI2HZiM1jc6KVmjylovdeQpTK88dEp8e2JFUwKLMV64kHZfifDwdleidLiobQJpMYc+ypTpa+eBHubbM8e4QgLwxsyrGPlDfjNq334CgeNdG+Q8q/ZuaQ5w855iMNODY0+bbuxOWrt8Wsa48FblTssI6K2wSsIWnGIpZUKHBbKnoworIV64nDOvbnB6wWR/cBx5lTeE5t/gHRtURNYaDqCwLJlyopy7RWcqsXApxt0mdeEXqLNa8MmjooXCQRVLMoO71j+6BDRSPGGwcqESwUwUoAoxVad07w4zlB4Lci5RtlOFAz+eHGvj4X0ruymmHZM7r3GwrUXWhwECcI/OyZ4LigGOtmq30HxYG6egnUFb0j6iQClVkbqPGvoVInQR/LyLW/YIWRHkW/Ib7uwFNydOicoLr1EeMEVCoL/yTHZlF2TsD2QQd2JhIzqinxbhbIyjOCc42NmConkK9KCiKfFHBVOWL5LKa354/U3Wy0EE6N/LHG0TJ9bQRLhMwohk7wPx9unmLU1JluHWR7XxxOEOGwgrEdDNTBQKRIRyQy4iKVhh6Lk0wjFrkwpnNcWlxEvNZ7ovI3Uvk88fCZJvJDiNFQq3OTwaJrNgad5OUljyUPReriJ3IvfiIYrjB+oqRArGZWvRopiOYFal4SPRyqMXHi+CkQNwWhTL6x9ilWdn8biQYqTgjK3xL5s5HKwYyeeoUyj0teL/3HzA5h65WQwzP5Wdjk3mdEXzspmaNWtr+Rh6KGswN2/BvFMGP+58MpJ1Z1EFk99Fgb20jdFMTItU+6WZQ9OMA2I4fewxAmi6i32yyQlyc4ytiaaZICHV5xMkFO3YtQhI00nsNC87uf53fDLy8+fJotlplxFFsqOHz409+9XMyWy/ndx8XmnW/vf5ldfr7bSHx2fbly/IsnZ555+nNc4XZ2Pf98ezG7GXbicTAmD/c3s9w7bG7PFaJaRiRRFEUFXiio6WTyk2APfhKKbUmdeGbhi9urmxv6u23DdyuiiYFRJNyNyVeWjUgAjpI7+lF65lsPj/cfH69ub6/e38wuFg+zq7/PctNVtiFOVcDMu3158j+NkBn1Pn/dWIo9aP1///0/659tX2j1i8E1rk3qzgJd/nJ183l2OV9cPsyXHz6d/ebnq5vFbLW5i2HHbofNWktvRSvul7PN/8eYsFhHlodd/Obpw1d+eX/14e+Xv9zffF59xfCEp599vLl/P5ztL09vM/zh/j8uhxP+5eHT/d3u519Xv5g9Jh/2afi7619spH6++cn93eXt1cPuR5t/eDtbLK4+rvbw3+9m/3gYPmh2/av3s5vlr5bz2+FInWVPjBTAeRXHPq9SoqZPxwYToKmUYhEp1OAS0+cPfxKL/kUq/iZvP/CYm6xRo7DN7etGgWUUNrPN35RRMKBj1qHFMRMlOUYTBT/DyU50UBd1EMB427qAY+qgA56ujv50D5tZ1WJmqas2aWA8qRKhx1gUcUCPrWz5SgpPagpPygRPFm+snYQR3bZasRtvnvEOb814KwDRqaMzECWBp9ujP12hhk61UEpDze9RmjJ0CXpU4fAeRxSNgoIR3bZXVzcKLKOg3hyiUyiiU6bFNRLRW2MoRKd0ogW2qAUAopNHZ1XKgTsqfYulocCGocCGOgQbXhYvp5QHdjQcfUcDarxlA+2wirgASiGnoaa+O510O5CiuMkwopOuG2/AeLu3Zrw1gOikPLZaagDRyaNTVw0jOtlC6iwVIdSeshohMQoJopNFX6ZhRBe7TeDbBP3mAJ1GAZ0ULWpB4TWtE19JRPX8hnFnvwkAdEenjhqI0JmjPxy9CdUtwiSgorGaknaCJVURS2oYzbUwDktdYRuFQrfViPLDryxe92oYzKlutwG7/ebuWw0fyx39EsLwkdzRcZxBcVyLhSNnCFIwL8Vsq6m7h7NNi9TOoCjOdmMAzD9+cyDOgCCuyUNSMTlHYTyjs9Pn81/Eh3BHj8gZPoKTR89kMegVaxMep0b+rKeqVw1cAm5WU/QOxVtE6Aa8YW3i4o7CqY7CqSZm51HnPwlFcLIjOMRov7n7VctHcPLoucIWTZhrunXwmhr0RgXEE9S0Gkt0OPmmyB0tP19OHv0G26IgTvZQHDKe6s2hOAuiuJZbK+MoGJdOWjhUQJ2dD5j/JD6MU0enqRath2i6q/ZUFxFPFT8kwGk1ZuFwi4vJapZ/19qcJ7NVl/3ao9S0PFcYDR98e3+9+vXsH1cfloPCfVMNmf0KEBA2pdt48uwTPUqcE9mxa/lPinzBHD0Q7ATofFS/G0acz5tDow6I6cWTNSMOjg62EMtA3QUkGHU9a6j6T3xiWWzRsjjNj/0ePUDhDP/hR88hcBZzE03p54FAQIYaTeCcyw4tyX+SAy217imYyMQq++YsNR/waXe6lppf36qPHv3YGwTOMyMtxYKBQptU13TnVbbNe/aT9gZcMz1fC3sMlBtzaet3KsTjbfKVxWtyz0cp+uh5pXuTiXmW2vQKGsRSx7dmqT0fp5mjM0DPx2nm6ElQe/NxedaopSODpfo4pqA6afiZ9p1IcLgvXtN7FLqZXg+NtFt+c0k7HkzPa+rPQvVeH44t1e9UZVvv5j+Jj+Ps0emgB3GcbUkGolpJGaqzsQsq21ox+0kBxXG2heJGj4IyS/U7875IcQMftdmjJ4wFFLXZ3skGMdJvDrWFfdS2GNbJ9zvauHLDaieJnJlqy95yx9DfnoG9eItMcm8E4s9Xi+XF8vHqbvFw/7i8WG1deSvsD9uKf/t2K6QSiWb8775mzO5WGn95PV+s/nd3Rna/fZxdXV9+uhp0cfW+w24sDv/G7uebv7qJdAigqWemf9x5tTFUViyWdSzduI9l2h8pJL1ZQnmPHHp0Xe7ouuzanrX/NregerX9/90Z0jM67ftbPKhhG1cdvPHj4/x6djm8wGDbF/P/nH2LDZ43EOloZ5628dQClyGyzoHMHqyxnAP2EC0XFXoOItIpTp3sOYiScw62kePR2uO0kVIsUsGoWJohRg6cIr9f396MLZ4/2h6XDqVKlkmyO8lv2+llxQIjXJH16tm1WTBte4c7WiUo906LKATTJnvks2t7dG39g73w6NTJ89WpGN7Zm4TDFItio+7IQlvbBcfrZdMesMmlqChdQ3ghWHskx8xMpOEj0ggiUi+QXnPxVBGpF0h3YHG6n/EMmm7u7z5erAzg7PqicrSVHzPZUuxBBF4Y+Ggbjm1Q444aDUeG3fPQ781o4Hkr5Tomrx9gwwYRxQYYXqC4UVkuiPCCFbrbLjheJTCZBnSl3Q6cHZHjDl6Ue+f5vfkWvNMmI5cBesmCY9virfGetkA3npWlwIjfm9fA9PHSjxm+pi3qiz5+c2gRH783FYJ5mEP3aFVxaX6USbniGddAv0N7snB8b4YDV1X1mOF42nW/rKoOVlVWdHDb7WK04YxMF9uyljjWjqiRIxHDbuHpJRrllJKNhCUaqpOqu4q6uQhsV6GL5EfCcFSwRb43xoG3tuPG471iXYGOnFaVKatCcZfttxFVXTL8QIIuxncUeudq+KrECqaZkTvvhMapJNVXFZ2X4l1/jpnLpbMnigBRwfFaBXQPPtncGK9ACCP5LocTuBo5WCz2BfUKxAmabdo0J2g18qSFTD/mxNbp0tw/vze+gLX3qjv7qhm1fGdvihBM8688TzfCojkFB2bMLtNKtsvUcPhTc1DZyG8yip1UvQavM3uCIXFU+XzelIXCCWrJUSfkHDYIrql0gFUaxY/8cIjmAEg58hzlTK/5JACpiyFZzW9cJ0+XgxgOopUjT3wptr71BoSrsme51A2e4zsGW8SrhlMiIUdeWpo2gjdp28xiBMmA8bt8YkDW9ht+SxR5ummehhNiy1/xjwVcOHa279YCIuDCcMCZ0iN3DLGoXyC2Uro7huph9ZLvGIqMwYAXs0qx89EMp4RCjfzWIjMVIO3BWYyrWg5W3MsPHYUR9YJvROGSCYtGQ/nZuha8VlX8CzzLibSpODI58xOWrIXlDJZKKn6erOXgGD1uJu7TYQnFts7eginwWvD3mpMBr0eedpZOTbBFlmFBf5uvnuso6LnNKz9l1pWlgt5vsgtJvWNdcI6beXun2a10vQM9uPZsa+NAD64df2mOB9duXB488Omug6/HHOd6TI+7GiUzPcEVwb4Db8z0jw6ljM70O77pL4YlHAp++EDTgRGPfLePbDqSA2GE4WfkONAXGsV+a8/xhcaO3CQkHRR84h190Tt60DsaPr/1oHc0pmcSVe1PtGz744vky7OScMYdJSu3MveegxLy3RLHcqkQ+X0WPIyyPH/Q4V671FO7WvKgE7adFRNnLvJNUxEaeU7wxsqRm6bi1YjnZOzYkXeAyoydSHJ4Qtl6g1jR8uMmgYMV7agLOiK/ON/DqWxI7/uTbXrrg2rrCe4Y9CzotqbNLv+mpq3lpuPogm3rG1l4U9fWzZC1p76tCyNr7cZ2f4VdiG3tmDhvGkVbT6H8m0bZ1jOmsFpj0w7OOYXbzm5TkVl7atoqyFlr27Yy6MIOu6bCZ9aLHqjX4uFmvqxVP7tfp75xY64PjfT95+XD5+Xlw+PgLYdnrrpuzH5enmXfIjRVuhZ2K7aU7Hl6s4IQLSs7Oo4VhGwph8t+fxCKK1L13SQahG4p5mBtlWlZ2XNWPlDazwOSePz4OGCN63q2/uq1tzBvs0X5LXGNy/vn5ed3xdU9vLpHXj40JWGzBBqbluZIVIqmXDSG4QxSNiUfspZuSxvKWwOpm9KbGM45yLaMGtYW2KYEksIWuKYMCdYW+KZrftbSoelWu7AFsekem+MU0a4s2/f02fdUsunujGNm0B4nOrBPK9qoQ/N9kjJNb+0ZB0zZpstEztlVrukykXXcfNPSrBMSmu4pWSckot7ZWMA7a9F0EcfZ78NmAew3Z6EW3XaDyDmDWqMvbvPckSUAAz9M1B9W2TPbFCLNO4a9+l7W3NFdyCq8bBZaLOaOBrRiNj69D3mUQ1Mtbsi/ZmzE24GjF0Y0YeLAsHJwOeXmtWN2F4xqes/IkBZaPaddRVrGNIGUwLAzxjY5f9bSrsn5s5ZuyyRiLf2sZtezD/NBLS4+3N++n9+trzQyFmWzIVL8mnf7ul30+dZl8T2uXZ6iHeiN7sOXy/X1xOXPj/e3lxsV38305V7krPewNog5rOpcClc7waYJzMOjFfdZ5ZvdaEuV9mGvNGu3q4TUw1bqLJnvXwhBs4m3N0UXUuz+s3dDdJ5ZjJDu5t7paQ213tpWqR5WF2cll93uvTIvno7509Ox31Z0rC7S46hYRYMoQW3gS1mnok3zoAuClI16I1+uNyW5/T571CVy1IENeEYQV4/z5afb2XIAn/UtsL+22U0oXNM/r/uy8/xTy7Dzv6z+0f3DbDj163c8+6cG1/LHs69fkc1P0wBqDsBqyiwZrlnSLxCm+KHC/OOeML+xUfuy+pcGWf0JktX6/BdkVfDubGEY0EeYV/ARf2zRqT9tDNSeL/nXBkH9teJM1nkoLxRjEZ5pTOIV1LVXeMr0HnJ6qMt6yrxFrka5xu0+cWftLNdZe9CkqE7tqOOYULtVqW/RdkSI2ln2UNToQlHoAXbqOnSEVtc4DSE0JwgT5iTXhEVQg0Unju8A/SR8TVxXMVeII9sU71WB41o5UagdQKjN1qq9CnSWVmnfoXY71GYnuSd2k4TaZS+41wmAJ2LboU8iDkVAn5V1LMpSQ9Dn8FkV6FOsnQ17PRp4QtfdW74DRKoIb+l13VtmGoMVBGlA5qbN9Iiyo+KAGZ0qbLdt3O4TJ8r88+ZwdCanjc6cR9FZ4J5G/wJhdAKb1wSFEVhHmRa2MMHsAi061G6G2s7zobYDoXYFdaG5BMqPw3tEpvfY62qDbcCU0ErarPjApHjuRZkH2bsKndpR0kio3aoRScl25CRVcSb8NtUxlHUMzztQZtoIzYMXl8FbrgbqFwijI7SstwkCQmheUeaULUww72BbBt+DJkxjSfi9GCQRNGHDEAsKUneo3Qy1PbunV/BgylDNCzpQxLJDn0QcjoI+lUxTHzDo4/jQJxaF7lF6IUbBr4LnGjYwhiBj91DvgDNNBHtiFHUPxRdkbDzJkyLKVOzNc2NvAc85kH7anClIkDMF7h3LXjs2XBidM+UND5Y4H6i0LL4wwewC6TrUbobagT3DOwQ0gaSMuvaaA/J8ldTT81XBUhrluRplGrf7xEFudExsFED2Lk2ndtRxTKhd0BXb4SFqF9i932MsGxk872Al8EkjNDQrNHDLRQJYLSFVp5nvAP2yFM0kinT5pjS8QKs61M5vvsWgNkVi+VoJVkDEjrTbkTY/VTug+SNlJxjB5gi+A59DaURBAJ9YEWWUEPCJ7HmLA0WxRaGDSRy2+9p3gEiJSMcgGVeV8vAXFNPb7vUT5zE3Nz2eTMkjq4P53dZtu33aNBk5bgbPDp42Y6pAt4L1cNzDaNtl0XF2QREMBLSjoSwLW5hobkEH2s1AO6OSRVduMO2tgi4wk0COw3dItu8ITd8/KaQSiSiN4N6RRYy4i87qKFmkrC6Ug845OdX8SOSzOllqcBQFnHEwbWwWBZhvEIXmqV8UslkUHZoV/IxEoNlaGeqmlC1LLN2g30sk1i1UAFakYiVSE7ESLgCJAmtQYDvEboXYOctadJUChdgVD4hVU/RYdioNU0c9UdiKKB2CepJn1VCPEkWZg+0TptdKO7PR57Tg8puNhSl6Kngiipr6GMoXKkn5wsD1hb5Ja04+GMH+fjhLYeKpP1FEkCxJwTUqsV0WnS3lFUEpjC1RPfzZwpRYPoHsgewXoOzIR9kBRdllxCXBMQzSTg9ySapbm7RchcLCDz0zmRZGQmpkJX84J6iKJZWKT2p0EZ5I3aZip47PFLNYMUo40WDixXNRojmB0nMtEFYcIXuLimSra/ZFkawvEqyPr1WuXas60i5sPlQGuTZsdWDAVkusYkL23Ox2pJ0xrkV9hlNGKjAA673QG45kJEcMh4yqYpuVwLBfALBfKAod7NOg1Diwn2ZOa1jvOnLqex/x5NzW8Eag8IamstP5kpRtR3lSkQIq9Ka4oTcFd2nsfQFJo+UhdKc0JUzDFaZuF+Y0CbBCO73xZYGlFajeb6QdaSv2bMhE2RhIuwi6FJhFoOI4QJfRXFft2jZgSq5aUQPLNNtVY9y9N9GmhZESO1c2HRojdsrziZ0p2xg452DiY06iQnMOtOQqYGyXRcfKBV9jMKxMER+2MDUWMNB9TGcii4qtpLzeIHhLBAzYKERjjQl0b6L9AqTNzx5RcPZI2QtqLJ+hj4ZMJaepfAZdyTLV0GjI5Fk16GNNUehY6YX23UK/A0RKXiFbqojGSq6FBltF6pG0wOBvgG3bgCkRZU2FQbXiQjs4Y+F5cHfH6YWjjuUGazLqEbjC9O3CnCYB1mhSF18WWGqB6ZMh25G25mePaI8i7QrownpAGNWRdiIOoglENOXhU9EYDGkDTSCcLgndgOMwjZ4gPKHarBjuzaCRbbt96mjYMWd3RwPnHBjb8RmBzyKEzwwFtg231MTodmFOE58ZNOeALwss58CYHjF5x3fNmmw74qhSa76JxMonjO9IuxlpG372iIGzRyqgC2uLYGJH2ok4HIW0K+3WTISQtnEA0o5FoYMtFKwYCfbjVhOZ0LYBU6IahhrvaCIXEGBs3soOCN4BFsRRgMALChBw9cbCfRqt6pyJMFpYFZ6l5oJb7gWFle3CnCZnsuiYQL4ssNQCazrSbkbaGSmWbKuVMNIugi4LhygudmhbMcVM6Ns3qoMK8g+HtvGiQY5/KOtbQQD12V5SmrJKYWGIix173Wz2i7WojgqOyWV+f0SgYakmipaYxialjoQDoyYP2PQngMZa6gO414wWHKxpwomfnx+AU+ndxy6WLH9YpjVcDPsc8VjcXt3cXMxuhk97HGzxw/3NLCfYLebRiOUKhqjeDrSqxbxu5b/qmdLfzq7nn2/pz3Itn6UdpZwpIKWi/M6klOXwMVKV8zItPrfxOfqvfiiS/X0Lhvrzoev95wYv8RPseqnz6eq0MliqkZgr9mmzzxGDh8f7j49Xt7dX729mF4uH2dXfZ1mBmm9OcyLA3Ys8Sa/R9KKy+2uCf//vv/9n/bPtC61+MRysdbxoF+G5/OXq5vPscr64fJgvP3zaYtxVHGcxWOTbYbfWG7gi4/fL2eb/g8JdN6IetvGbpw9f+eX91Ye/X/5yf/N59RXDE55+9vHm/v1gLr88vc3wh/v/uBysy5eHT/d3u59/Xf1i9ph82Kfh765/sfEq55uf3N9d3l497H60+Ye3s8Xi6uNqD//9bvaPh+GDZte/ej+7Wf5qOb+d3308yx4ZB2YPPJ2YAwPgjhjU/PNeGG5VidsUy/vpm8jgXjAPWeQve4uYvVfR0Cr7QdrnNRwUVrSBj+W4UM2BQyGN7FDNScq8Y90DnWRDNcdtwuEU7tjV1CmzMxRltsX9xkMUz2muHUixj/uhpnkCSFHlhusF8hI1KC3QsYUWWCovzfrkpSl46HVCC0IRMTqUrYse7WGcTElFe9asrOYWLBXtoYaV2UqBJ+3EuKOSnEMZx67SqzMOnhUMb45xgFkUTyemM44fyjicZjMOvrkIYBBRhya3SnUKcUk4jjKJW5Od/6qI4z87dbztiQJVaYvozGPdHy52TQMmDVq8IHTCk6DFElzWEyHt4GzyE76R8RRo8dysAQ/GPbTpcQ9697EGS54f9/DcvGuPxz2ee/x0Hs7e/kPJ15vBBEeVE/tiZMVrmIerBsCw9uDYXVtw1PVcSDMKQ7Fy0xsUGMkWYOSo21VHNRpJbxg3biH/VRaF+mKiUH9dMfxqUN/ziyj4ThaPDIgeGUDssnlrkQGP9ci8UL7jMk9RXY9VynjPx2WRi8vwRBMVps6PA1GOKMtpID6CeuQ6P84c/HPquB8CIUfUIPhI8ePD1LXgDd8zU5YgcHsVB4Hrq+k8ivLXVGeRUI+IBU8yjmK5apAoj1JN2ZuemnXlA3p7GaNIeVQxFBsUyKOUafpOIhoSPHVFGEzefOS/ChwOebGbkDM5HiVlEK9IpAI/455vjQ1KpHbS70SKh7TUWyNSweIOXE4dcEdBAe6y13Eg4BaduAaq/UPwEHEN7BYPycplvwsGJGTsRCqzu+eUpBIk5AlZE1wteCrO7X3leJAnk5tgHfDAx/P43U6k2Op7yBjqpiIEqhdALEs0gvxC+iZ+QRzBEKh7mqjyWpX9qihQeiib8nJI9hfSn1hKVj6hh7Fo0CPYvfFiN9q8E6kfTKT45S5saxwVSqSk60QKMczxrRGpqEEAqDuwj5pyTQ4C9lGzgX10TGAfDQ7MzOQJMtVUxJdNLx6QWDXp6UC4LhCKqMRAAGEKj8ViyCOCIQ+pOjXOmLJzTKKDjhF3jJEg1yG5eAiZcEjRwJK2ndvtOMKNN2RTxhsVKkivl9bOod4ZULiUc7jil4JNMy/iVCmHWyH0V6Mc0fLVgH3K4XCBaDrklgoXULkLQoi8qcl9llx3WMWoVOxMCvHsb41JDUcGbpt54SeOuNeOpg65Q0VHsd6YF7YDtM2mEYZSU7cXgeobLIgS/hB18hPJdU7pG2a+gTntZrMWcojc5OMfrP1XSAQkd+Yq0le8GMjmFKDlUp2TkyabtiBE35JoSf7hy0K1aCFRC+CMRE1YIImsECFvOAuf5eA+jU3fJcmtl/h9lEw6sgzrlD8V7Y+ges3Uj6eLqROtumS+ww1wtl9nVpB9tm+PWmH1Hr2L32bL6v5JohgNGOYp2RhNwqUYYvKkWVKdRWJlv+EoRYfEtEBISCzrLQSiIHGZtGWZYoGQflGVtWbnqFAllVCdMbEHWJriUiH6GuiibbzkwjKJNqJooVWRCgxlb56koP6RSmNUwpQ/Fa03sR2AQtbQvTkAKsE+H3aySZWvecOZ2rsaZQVsIzgZpC0yQ1XP0lFXafIuqvBVHkWC/bpKUT0LivlEw34HCKX1SpvtnhFnnsJxMhoKpVFJYiLpUS0cYGdIlKYU2xJhgZA+eYqz/TJggRCJBEICNxCiBOZkmrLFoqCG90hBnladV7HCZ6GNGZoShBKFlIw7irUHJIhFOmpLlC28gtsz9hxgBp0gfYAyRHCF5PqqcoA1yBZlv6/AMJV4c3RRGYwuyqnecEqzGof4enxRKT6O46M0BReDTL72Zu1qq7BLiXIAXGG1GtJ2XLzeM8KtegwXK8fHxcqzcTHWokL2Vn/Z7T0nhXU4V1UoSt5U5UkCuaO0gL2lD2hgW2S4T0VvU8Ew2eQp0/UbsihJ2qbLAUwVUWrZ0qoiObOc66c1BCA+LO0zLssHWINTTOVka6zWA19fEVEGwMKx7ZeWKAnt5UiQKdPqzZFQDXYKbep4E6ksiShpJ1HAHoXPgmeRTr7z39rZ1O+tZDnhXhssu0h1crXeM+LQW4xcacMnV9pyyZXGpqOqPmcsu73npLASA+coeVNtwRQ1tUjG2hGhD6hngxO0dKWpJfXG8kNbwrnPEcamOLwcadJw0kRvHM+QLKlRhiCSikwsNGUiqcGhnU2t4yN1jxUVrZMxb0gKnxVB0qB6Nzjs2IY3RxoMGGdQU20fqfyrJjpqzw8z8D25gYtDJj/GaA0g6txKlT2PASs3YudW6z0jwILGuJVRfG5lNJdbGayzhBadW+W295wU1iEkkp6SN0UkNMWtlK0dEfqAsqulDdzCog/8ZZhs+pQ5gm+QKWWmDMyNRWutmnI9NUmHjcRvqYRN8z9V5QA7DFBq3QHlawBKAzR7AMyXBymo7pOdMEv2BikoGI1pGoi+OpqJU6fGbmhiKN4WehQ+K8Ke3E6eW1mq04Eqh2qtwPB37+y22bM6MLIS41ZW8LmVlVxuZSUmW9+5VW57z0lhHRo4FSh5U+3DtEl+ovnQg3FA2WnaFi7X0aFzK9Jk06eM6IWiyaRAW7H6cB+L0AYfbMqmInX0qc6qwqXlq+u8+MK3GhApxSYaSd1baTLeYV3ekBQ+C2y2YMRkKaN8Vc5ogeoZwCw7kDMa0TkjZKHNm+OMFk7LMGry5MoR2F3piuvBmlmYPjZss2d1P+kESK4Cn1w5wSZXcKTC2I6LSW0jmYsjJh+RN1+bFfJCdVg0xJjOmHP6dY5KVWnqNtIRpDua9CdAsJ62OjZyoZlDm3kY20Su0iumtYev7xI51MqnE4B0ue+DUyAL8VNlIeveka/IQiKgDPyjrsGeb66JW1NN3wyZGetM3uQUPgvtfWl8J1eQm9dvjlw5uJ2FiZMnV57oDaxMxfVg7Sys6ORqvWeEoQTbWTignYVjt7NwWDsLKzsOz23vOSmsQ6doSHmTCJN01rVm3YwDyi4Hd3A7C6s6QyddN3nKPDHJnbw/Fb4iVHCUqm3qwG6pem1DnlOv8sqV/ywvQM5oW/J5oon43doa2dSbx+ryNZWXYE9wM1GCqMOrjrFyQEcOvgn2Ch0iYDqRgqzx25sQ7J9jCvO7n+d3w28vPnyaLZa56X5b3j2w+6e/fLmYLZfD8ovNWb+9/2V2+fluYylm15erU7F4Qle555u95y+GD8mOW9s9mUfdkGNbpWhl+PnbM5R7lVPvvQVE4L6DCBxLBG7cIog2nRHp0+EENdTgATmJ7yCnwH/+Lq3mqM+PrHMixq6qIY3Jm3JyVxCcXdnJY8QG7LDOP7pytChI4Kjq4x/VoFhC0aM/qhURAI59V65wVBGwHPvuySMWQcJWfVqMZsu3HwHw/rsmH0eVkwOe/x3QR/Ccc6Lc6M9JOnrblYvwQ2Dtih05Jgtp/CNUVCXyj6r8DgAosly9HL2rr4xqjYBj3zVvPKoIWI599+QRi0AkI+5TVOrKgcAIeH/5Hbx/NMDz5Xd4vmWdk9Gjj5h2bK6E8yOL6e/kMeJdsYn2lL1KBGj9d8BfkeXpR+7opRRlrBMBt26OLoDhzVhhjbHrRGaIcUwhaSi6fin4rl9/Bykp9tPVd3i6ZpwRNXodNWXhc9j86MMp6Ty+QfLpZMGKjvDJfPwOp5Tj3uPoT2kobz/flUvxHfaf48rl6OPjucn2KQyNFTHxHb48/pWjlIL/ePcdHi85p2T0F56ZMaUyTdIpD1CTkkP15djjgpUBO1KyUIce/Q5UzgA/jKC+A+iUnCiCMqMXgGZNgvJlMfHvENqvMLb5M/tJaGmy0fPMpWFXbu+vV7+e/ePqw/Lmy9le7tnfCt/BuYvYD7q/koR/d4YNh+A3s9kq4/nZIIPHx/n17HJ4hQ9/H978P2ff5iLu7Ro/L0F9B/4u+WhCxRM+fIoTh1BxbIfPSP7hUwo+fIqDpvToI5qZiSCqTEMVBzrpsRORVRNzftdXqfhXIvo7kEPFhzJafofHc6CMdqOzLhGwLh63Lnxgo90p+xYOsNF+9AbBAq3KpOLjFv0dwhCKk06pR3+TnWvNXWYSmh+b0cdPL5Caf8dhvgOU1fxLDmO/w+M58QYzerpbbrAhNeeaw4z9MjbX0lHrtGVD2XRq/j2H/Q5gRnMuOqwc/UEth9A1/6bDfof7UM256bCjz67JdedJ24aaij159vGzfzw8zhaLi+Xj1d3i4f5xebEqzqrUOrkftm3/9u22rSMRB9V3/7tffTe7W5UVXl7PF6v/3ZWh7X77OLu6vvx0dXe9eqflsCWLw7+x+/nmr27ArOCj/mjZc2ejLZZdyb2xcrBs/EHBev4BkpVYYrPiVuNgYNECjbI3NXAQAdsbRsYXktsJKb+kbl/yQEgu/wAg93GHptwpskbDSqI0Mr83IznADmgY7CN+gIHyil3/19M8DB5Xm13Vm2epTWh/QPeVxeNt2b6ynE4uTQuOEXnHln2AFe0PKNj5vXkc/POkf7QtG9t58uzZKdGXcbFtcOvaANjL6vYHHBqT/ANM++nifYFteICqa4RrX5KFfCyrlk/LUSNeB/T2DAYGDBao8lfxhAGDBdL6tTjhD9lrU31zf/fxYmVfZ9cXtbpMP2pI7IHuRAG/VHMNjllZwAy5Bu+iXEeSxKmIbM9fqSJxul34BbfmTLu4Wa7YNbhiGQH061z7A0qb0kDXdmWzXQdKOhA8XwfKtyd7rTKZDkX6UUOmYPkOJeI5YC62n3VWaMILoJrZnjCU2esPyT15etRQJgJTKSKe+uobkIZU3coSQmN3uY6xbGV9A9KQEoCZ3rQLn4U7vG3/At4DWnCHQLbItz+gAGx8Q5gYAXs+Nq/PChyFhkin7VFJIg9UKH5j/ErNWUip6eLhZr6sNmXwhxMl1M6JH7rubb/wh8dBVMODV1549vPyLP8qvBZ2Y8aFgyiA4oBNBwnIPYeWq17AvAXTvH7BukHd4E4YaAbcs+QdV8GI+tbleTY6AGZAfVcrgHsjXT1gEXc/qnsfwoxJwPvIckZSlK3CZlkrVu80M26HIgXgUPDLGaCt2imHASLut3qiBXn0gMG3SpSNgG2VDctzxgbHjDC+mHrmz8NpfPz4OJzXa+IJqy/YHouNk8w7RVbLNClHbsk8YMkCbsmAHiwnDDSVwPFMIZju8uvLlvPskfOsBB5FlP26klIg5fn2WBcvLJXQzcLhGGQl+NnCMp6yInKShQs3jKMxysoCnTQkapSVwJ2z0t0QUO1PLGAIQtkQ4DEHpfhJAEqEZuF71vqx+f1Z68uGyAIQbFMSZ8fPiSOc9VXz+rz31837k4/lKInTOBURidrm9VknXuLmTktEor55/W5Oyy03NN+cmrI5lbi506KuDrF5RdZxVbiBQ7KnlZLN67PUQeEGTntkf3ADpx2yvml+/8KJUbiB00CwRakGAxcAA6188/vzdjw0v/+PQ/ijM6BW8g2oLdbQKIWbu0JJVv7watG8PsscadzcGYW8P27uDHCdorRufn+WcmvT/P4s46Rx42cMIl/c+BkET2vf/P79KrM8mVrwjZPTReOkQ0PY1FgobKo5DbQKlfujiThZ4BpAwxeayvAzm/f7kpxc9NHgzsR2qkcaAyCE7oqZuCrTxIM2BjaPJdSTaZjfFS1DpsUH44GSeGDNFhlO4zA78mw9B0S/dcBtEQ5IbLXgWRnXvCILghigC5c5Zev57K0Xt1c3Nxezm+HDH+cfLh7ub2aVfjgRncBeNBGxNaEvcLB0Q3uJmF0+D6UbWk3E5w2k3169IKcifOVYzIZ+CbsHxLxEGxok7O5NeXtuX3AxH3mb4po/IbI+wTcHzHinPjSvXxJqbA7BRY5BdaJ5/ZB/44Zi810Ii/fGqnn9wFpfN4f4WGrUUDytI7I/tjmKxFvfNUdJWDrk/AuILM/2utAcyOB9QmxNkVIir1RetBrGVcv+b994gJAroDMs9f7m8+zhcX63+tcDalys/4LXQjrn1WCMv379fzvT+cA=
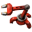

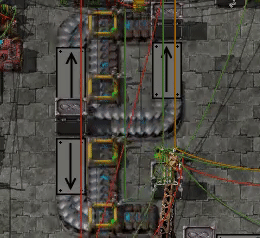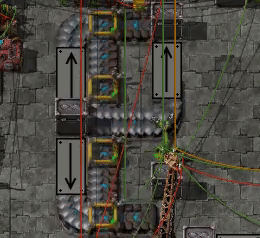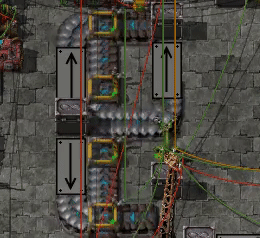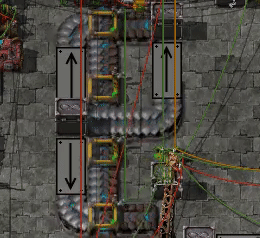 6.92 items per second:
6.92 items per second: