Flow Routers - UTU balancers without the balance

Circuit-free solutions of basic factory-design to achieve optimal item-throughput.
Involving: Belts (balancers, crossings), Inserters, Chests, Furnaces, Assembling Devices ...
Optimized production chains. Compact design.
Please provide blueprints!
Forum rules
Circuit-free solutions of basic factory-design to achieve optimal item-throughput
Post Reply
Copy link
Scarab
Burner Inserter
Burner Inserter
Posts: 10
Joined: Thu Aug 12, 2021 5:31 am
Contact:
Contact Scarab

Flow Routers - UTU balancers without the balance

Post by Scarab »

The Flow Router (FR) can be characterised as a "Universally Throughput Unlimited" (UTU) Belt Balancer that may or may not balance inputs or outputs. It is a sister to the Balancer, not a child of it. As a Balancer can equally be characterised as an input/ouput balanced FR that may or may not be UTU. It is possible for a block to be both an FR and a Balancer.
While the purpose of a balancer is to ensure perfect distribution of supply/demand across available belts, the purpose of a FR is to allow for perfect flow of items across available belts. That is to say; the throughput will never be lower than the lesser of supply or demand regardless of input/output combination. Routers have the added benefit over Balancers of allowing for much more compact designs for reasons which will be addressed below.

There are many situations where a player wants a number of belts to have the UTU property so that as long as material is avaliable, machines will run. Most prominently does this apply to the Main Bus systems, but it can also apply to any smelter array, mining outpost, or large scale lategame factory. Currently players use Standard Balancers, possibly ones that are UTU if applicable. However its usually the case that even distribution has little to no effect on the factory. It is in these scenarios where using a Router would be preferred and result in improved factory throughput.

Image
The Flow Router achieves UTU by ensuring every Input Splitter has a minimum of 2 distinct paths to every Output Splitter. Distinct meaning they never share a belt tile or cross in a manner such that the flow of one path interferes with the flow of the other. As all Splitters have 2 inputs and 2 outputs they require 2 paths.

Creating any Router f(N) can be accomplished by first establishing the factors of N; where N is the width of the Router and is not a prime number
U, V such that U * V = N where [U,V] =/= [1,N]
For example
12 = 3 * 4 , 2 * 6
Where multiple factor pairs are available, the combination with the smallest total number of Splitters is advised to lower the UPS cost of the Router.

3 rows, each comprising of a group of routers f(x) in parallel, are connected in series. The 3 rows are:

R1: U * f(V)
R2: V * f(U)
R3: U * f(V)

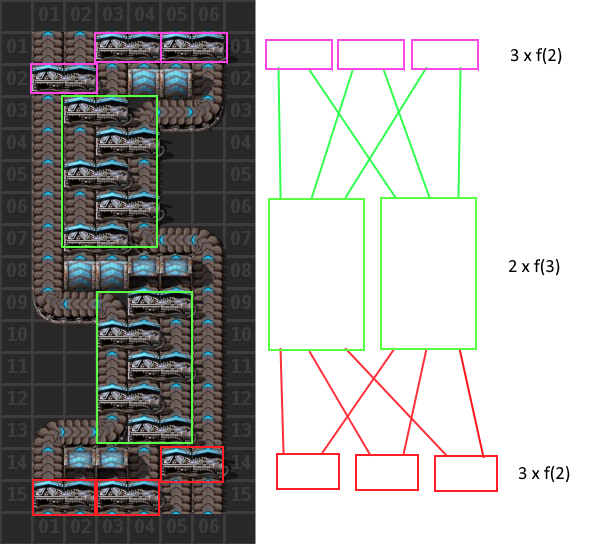
Image

Where U * f(V) means f(V) routers U number of times.
R1 to R2 and R2 to R3 topologically are the same graphs, except one is backwards. This matches the common wisdom of pasting a balancer twice in order to make it UTU.

Thus the number of splitters in f(N): 2*U*f(V) + V*f(U)
Minimising this number will give the Router with the smallest number of splitters and thus the lowest impact on UPS, though it may not have the smallest possible footprint. It is likely that the Router with the smallest footprint is one where U and V are closest.
Using this formula we can choose the correct combination of U and V out of all possible factor pairs of N.
Note that as in the example of N=12: U=3, V=4 does not result in the same solution as U=4, V=3. It is important to check both orientations of each factor pair.

When connecting the 3 rows, each output end of each indiviual f(x) in row R must connect to every input of each f(!x) in row R+1 exactly once.

This requires that for any Flow Router N to be optimal all Flow Routers corresponding to factors of N be known.

This method can be verified by example of the standard 4x4 UTU Balancer we all know and love. Notice that its factors are 2,2. f(2) being a single splitter.
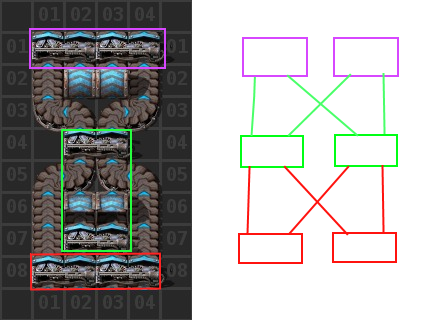
Image
Notice that the balancer totals at 6 splitters. 6 = 2*(2*1)+(2*1)
Notice also that the balancer is constructed as 3 groups in series of 2 splitters in parallel (topologically).
Notice finally that this Balancer is in fact UTU and thus reaches the same conclusion as the outlined construction method.


Using this method of constructing a large balancer/router out of smaller ones means that whenever the design of the smaller build is improved, all larger constructs that are based on the lower order design can be improved in the same manner.

To this end, since a flow router is not necessarily a balancer, Splitter Priority can be highly utilised to shrink designs of routers without regard for the effect priority has on preferencial output delegation. As an example; Using this technique, the 3 wide router can be reduced from 5 splitters to 3, while the footprint of the 4 wide Balancer can be reduced from 4x8 tiles to 4x4 tiles. This has a cascading effect on all Routers where U or V are equal to 3 or 4.

Image Image-------Image Image


Updated Book to include 7,9,18 Router. Added L turns, removed U turns since they're really not useful.
FactorioBin link



Deprecated:
Here is a BP Book that includes the routers I have built thus far, including versions that do and do not use priority, as well as U-turn versions.
FactorioBin link
Last edited by Scarab on Tue Feb 08, 2022 3:54 am, edited 2 times in total.
Top
Tallywort
Inserter
Inserter
Posts: 22
Joined: Thu Mar 25, 2021 11:57 am
Contact:
Contact Tallywort

Re: Flow Routers - UTU balancers without the balance

Post by Tallywort »

Interesting, I have a strong suspicion that it requires the same number of splitters compared to 2^n balancers. (and if not, it will at least grow with similar time complexity) while allowing somewhat smaller designs for the other sizes of router.
Top
Scarab
Burner Inserter
Burner Inserter
Posts: 10
Joined: Thu Aug 12, 2021 5:31 am
Contact:
Contact Scarab

Re: Flow Routers - UTU balancers without the balance

Post by Scarab »

So I've found that making a 2n+1 Router can be done by adding 4 splitters to the 2n router IF V=2
I've made a 7 and a 9 belt router from the 6 and 8 belt respectively.
Though they do need a few minor priority adjustments the extra lane is pretty simple to add
Image


Though it stops being inline and the 7 wide actually shifts the belt block by 1 tile it does unlock a new minimum number of splitters. (Maybe someone better than I can reform it to be inline without becoming too long.)
Making a 9 belt router using my initial method would result in 27 total spiltters, this 9 belt is 24 splitters (4 more than the 8 belt splitter).
The 7 belt balancer is 4 more than the 6 belt (16)

That is to say making a Router i(2n+1) with this method will have i(2n)+4 splitters.

Essentially what the extra lane does is connect to the entrances on both sides of the first Row 2 router, then "bypass" its way to connect to the exits of the second Row 2 router.

_____________
Tallywort wrote: ↑Wed Dec 08, 2021 4:08 pm Interesting, I have a strong suspicion that it requires the same number of splitters compared to 2^n balancers.
As far as I can tell the splitter count of all i(2^n) routers is the same as the same order UTU balancer, though the footprint of the router is the only advantage it has over the balancer.
Top
adam_bise
Filter Inserter
Filter Inserter
Posts: 437
Joined: Fri Jun 08, 2018 10:42 pm
Contact:
Contact adam_bise

Re: Flow Routers - UTU balancers without the balance

Post by adam_bise »

Scarab wrote: ↑Sat Nov 20, 2021 7:59 pm Image
What is the purpose of the priorities here? How would this differ in terms of throughput if the priorities were removed?
Top
Scarab
Burner Inserter
Burner Inserter
Posts: 10
Joined: Thu Aug 12, 2021 5:31 am
Contact:
Contact Scarab

Re: Flow Routers - UTU balancers without the balance

Post by Scarab »

adam_bise wrote: ↑Mon Feb 07, 2022 9:09 pm
Scarab wrote: ↑Sat Nov 20, 2021 7:59 pm Image
What is the purpose of the priorities here? How would this differ in terms of throughput if the priorities were removed?
They incourage the items to flow through the "bypass". Its necessary when the input is not full, but more than 1 belt. As an exmaple; If the inputs were on belt 1 and 2 and the outputs were on 1 and 2, without the priority, the left lane (the bypass) won't be saturated. The reason why this is necessary is the whole "2 paths between every splitter I/O pair" idea.

Image

___

Also an update, I've created some Corner routers, and replaced the U turns, since I don't think they're'll all too useful. Here's what they look like.
The set of 8x8 still needs some work

Image
Top
Frogbeerr
Manual Inserter
Manual Inserter
Posts: 2
Joined: Tue Sep 26, 2023 1:24 pm
Contact:
Contact Frogbeerr

Re: Flow Routers - UTU balancers without the balance

Post by Frogbeerr »

Scarab wrote: ↑Tue Feb 08, 2022 3:53 am
adam_bise wrote: ↑Mon Feb 07, 2022 9:09 pm What is the purpose of the priorities here? How would this differ in terms of throughput if the priorities were removed?
They incourage the items to flow through the "bypass". Its necessary when the input is not full, but more than 1 belt. As an exmaple; If the inputs were on belt 1 and 2 and the outputs were on 1 and 2, without the priority, the left lane (the bypass) won't be saturated. The reason why this is necessary is the whole "2 paths between every splitter I/O pair" idea.

Image
Wouldn't the backpressure of the input force the throughput through the two available outputs even without the priorities? Yes, in the begining the "bypass" would not saturate until the remainder of the FR gets filled.

Basically as soon as one output of a single splitter get's blocked, its throughput becomes one belt. Ultimately the splitter labeled 1.25 will only output 1 belt to its left and thus only accept one belt worth of inputs. At this point it will no longer be able to consume the 1.25 belts worth and the remaining .25 belts will overflow into the bypass, thus saturating the bypass without priorities.

I would love some clarification, whether this is an edge case or if I'm just plain wrong.

Props for the maths though.
Top
User avatar
Gergely
Filter Inserter
Filter Inserter
Posts: 616
Joined: Sun Apr 10, 2016 8:31 pm
Contact:
Contact Gergely

Re: Flow Routers - UTU balancers without the balance

Post by Gergely »

Scarab wrote: ↑Tue Feb 08, 2022 3:53 am The reason why this is necessary is the whole "2 paths between every splitter I/O pair" idea.
Image
What would you consider an "input splitter" in this particular case?
What are the two input belts on the sides that do not immediately run into a splitter?
Top
Scarab
Burner Inserter
Burner Inserter
Posts: 10
Joined: Thu Aug 12, 2021 5:31 am
Contact:
Contact Scarab

Re: Flow Routers - UTU balancers without the balance

Post by Scarab »

Frogbeerr wrote: ↑Fri Oct 13, 2023 11:15 am
Scarab wrote: ↑Tue Feb 08, 2022 3:53 am
adam_bise wrote: ↑Mon Feb 07, 2022 9:09 pm What is the purpose of the priorities here? How would this differ in terms of throughput if the priorities were removed?
They incourage the items to flow through the "bypass". Its necessary when the input is not full, but more than 1 belt. As an exmaple; If the inputs were on belt 1 and 2 and the outputs were on 1 and 2, without the priority, the left lane (the bypass) won't be saturated. The reason why this is necessary is the whole "2 paths between every splitter I/O pair" idea.

Image
Wouldn't the backpressure of the input force the throughput through the two available outputs even without the priorities? Yes, in the begining the "bypass" would not saturate until the remainder of the FR gets filled.

Basically as soon as one output of a single splitter get's blocked, its throughput becomes one belt. Ultimately the splitter labeled 1.25 will only output 1 belt to its left and thus only accept one belt worth of inputs. At this point it will no longer be able to consume the 1.25 belts worth and the remaining .25 belts will overflow into the bypass, thus saturating the bypass without priorities.

I would love some clarification, whether this is an edge case or if I'm just plain wrong.

Props for the maths though.
Nope, I'm the one that's plain wrong. The particular example I gave here with the inputs 1, 2 and outputs 1, 2 doesn't actually need any priority to flow well. It seems I wrote that "proof" without checking my notes.

Image

From Left to Right, we have a real test trying inputs 3,4 leading to outputs 1,2 with and without priorities.
An initial look shows that without any priorities it doesn't play nice.
A first attempt might be to add these two priorities to the centre splitters. It functions for this particular iteration of inputs and outputs but the big problem is that since the router is symmetrical, our priorities need to function for both sides. Meaning the priorities need to be mirror-able. So we can't have any settings on the centre splitters.
The prupose of the first output prio is really to ensure the splitter above it to the right only takes input from lane 4 since theres only one path from that splitter to the output, only one lane of material is allowed to go through it, so we choose the lane that has nowhere else to go. So we just give that splitter input prio instead.
The next centre setting to tackle, functionally forces lane 3 not to use this path since we already noticed that its the only route lane 4 has to the exit splitter. So again we tackle this directly by rerouting lane 3 straight to lane 1 onto what we could call a bypass. It now has a direct line to the exit.
We now have a setup that can be mirrored and will work in either orientation.

Unfortunately this doesn't work for all 3-3.
We could tackle this by adding an output prio to the centre splitter to the left but we already concluded that centre prios are to be avoided.
Instead we make use of the right hand bypass on lane 4 which comes already saturated with an input prio on the output splitter.
This cascades the other lanes into saturation and can be mirrored so we finally have the finished construct.

This is the MINIMUM number of priority settings needed to create the first 4x4 router, but for complete transparency lets delve deeper.
The reason fundamentally that the priorities affect the throughput, is that it forces the router to always either use 100% of a path or 0%. Anything in between gives rise to deadlocks.
This means the logical conclusion is what you'll see speedrunners often use. They simply fill every single splitter with every same sided prio. And it works! For any size zigzagger.
Image

___
Gergely wrote: ↑Tue Dec 12, 2023 7:59 am
Scarab wrote: ↑Tue Feb 08, 2022 3:53 am The reason why this is necessary is the whole "2 paths between every splitter I/O pair" idea.
Image
What would you consider an "input splitter" in this particular case?
What are the two input belts on the sides that do not immediately run into a splitter?
For this blueprint, input lines 2,3 are the input splitter. The point is that having 2 points of entry necessitates 2 paths to reach 2 points of exit.
It's a rule of thumb to help design, and I'll explain with an older 8x8 balancer I found.
Image
Standard non UTU balancer here. As long as all the outputs are active you would always get equal product on each of the belts and part of the reason for this is that every input is connected to every output. Lets pick 1 input splitter and 1 output splitter and isolate its connections.
Image
Its pretty easy to see straight away why this isnt UTU. Only 1 belt actually has a path to the exit.
To wrap this example up here's the same balancer pasted twice as per the accepted method of turning a balancer UTU, and an example of a seperate balancer, this time its 8x8 AND UTU. The two distinct paths are coloured for reading convenience.
Image

Image

The real answer is, for however many belts you want to run through a router you need to consider each input abstract router f(V). However wide this abstract router is, is the number of distinct routes you need to be usable simultaneously between the input router and the output router. A router f(2) is just a splitter hence the guideline I gave being 2 distinct routes.
And here's my 12 belt router with all 4 routes since it uses f(4)
Image


BP Book update, I still haven't fixed the 8x8 corners :P
Top
User avatar
Ranakastrasz
Smart Inserter
Smart Inserter
Posts: 2171
Joined: Thu Jun 12, 2014 3:05 am
Contact:
Contact Ranakastrasz

Re: Flow Routers - UTU balancers without the balance

Post by Ranakastrasz »

I've been using those smaller splitter bricks with outward priority instead of 4:4 balancers for a while but I always had the output side prioitized outwards as well. It never occured to me that not doing that would add a bit of balancing back into it.

Why not use the expanded brick design? Is it just for extra balance, reduced UPS cost, or what? a brick distributer always fits in an N^2 square

https://www.reddit.com/r/factorio/comme ... _maximize/
Image
My Mods:
Modular Armor Revamp - V16
Large Chests - V16
Agent Orange - V16
Flare - V16
Easy Refineries - V16
Top
User avatar
Yodo
Inserter
Inserter
Posts: 24
Joined: Sat Dec 30, 2023 4:27 pm
Contact:
Contact Yodo

Re: Flow Routers - UTU balancers without the balance

Post by Yodo »

Your 8-8 design is a lot smaller than the one in the blueprint book posted above, but uses 8 more splitters. Too many splitters is bad for ups, as they disrupt the transport line optimization that Factorio does, but I don't think this will be a problem unless you kilobasing or megabasing.
Your design also doesn't use express undergrounds, which save a lot of iron ore (2396 without productivity), but the larger number of splitters means that it uses more of every other resource necessary.
Have you considered using flow routers instead of balancers?
Top
User avatar
Yodo
Inserter
Inserter
Posts: 24
Joined: Sat Dec 30, 2023 4:27 pm
Contact:
Contact Yodo

Re: Flow Routers - UTU balancers without the balance

Post by Yodo »

Apparently flow routers have also been discussed earlier as "compressors" (in 2018). See Finding balance: a guide to Factorio belt balancers the document has some nonstandard terminology, and was written before priority splitters were added to Factorio, which means that, e.g. universal balancers were impossible to make (with just belts, undergrounds and splitters).
From 2017 there is also a Reddit post by Raynquist about "throughput unlimiters" (FRs) with a BP book that has been lost to Pastebin time (an image still exists though), also pre-priority splitters.

Since the "expanded brick design" always fits in a square, but uses more splitters than strictly necessary (see the earlier designs), can flow routers be made shorter than they are wide? :D
Last edited by Yodo on Fri Aug 30, 2024 8:07 pm, edited 2 times in total.
Have you considered using flow routers instead of balancers?
Top
causa-sui
Long Handed Inserter
Long Handed Inserter
Posts: 69
Joined: Sat Sep 12, 2020 4:23 am
Contact:
Contact causa-sui

Re: Flow Routers - UTU balancers without the balance

Post by causa-sui »

Could Factorio SAT be used to discover better designs for routers?
Top
User avatar
Yodo
Inserter
Inserter
Posts: 24
Joined: Sat Dec 30, 2023 4:27 pm
Contact:
Contact Yodo

Re: Flow Routers - UTU balancers without the balance

Post by Yodo »

I think Factorio-SAT can be used (if it can handle priority splitters; I forgot whether this is the case). It takes networks and tries to fit them in a certain footprint. Doing this iteratively will let you find the smallest footprint that fits the network. But finding the network that will give the smallest flow router might be hard. As shown above, more splitters can let you make a smaller FR, so it's not a question of coming up with a network that has the minimum number of splitters.
Have you considered using flow routers instead of balancers?
Top
User avatar
Yodo
Inserter
Inserter
Posts: 24
Joined: Sat Dec 30, 2023 4:27 pm
Contact:
Contact Yodo

Re: Flow Routers - UTU balancers without the balance

Post by Yodo »

Since compact FRs seem to be boring (but maybe 256-256 TU balancers can be smaller than a splitter square, as the 128-128 balancer can be done in 128x73), what about lane flow routers?

I actually needed one in my base, as I do a lot of side-loading off my bus, and my iron outpost was running dry, so the Madzuri unloader started limiting the throughput.

The smallest 2-2 TU lane balancer I could make/find is 3x11 and uses 5 splitters (TU lane balancers seem to be less studied), but since I don't need the balancing I think a simpler/smaller design is possible, and managed to make the design pictured on the left in the spoiler (based on a design by CrusaderDeleters):
images are large
I'm not completely sure that it is TU, as I wasn't bothered to check every combination of input and output lanes manually, so I included the splitter network diagrams (based on the ones by ones by Raynquist) so it can be verified by hand more easily. It is TU, see this Reddit comment for a diagrammatic proof by Raynquist. I included the "dummy" splitters in the diagrams, as interestingly, my new design uses one less splitter than the TU lane balancer. But it is wider, and with a rectangular footprint of 4x9 is bigger than the 3x11 TU lane balancer if you don't account for/use the empty space below the "bulb".

I also tried using a 4-4 FR, but this used even more splitters, and only fit in 4x9 if I used hood-loading onto an exit (which means you can't paste multiple copies right next to each other).
Have you considered using flow routers instead of balancers?
Top
causa-sui
Long Handed Inserter
Long Handed Inserter
Posts: 69
Joined: Sat Sep 12, 2020 4:23 am
Contact:
Contact causa-sui

Re: Flow Routers - UTU balancers without the balance

Post by causa-sui »

What makes compact routers "boring"? Making them smaller means they can be applied to more use-cases. 128x128 balancers are impressive but practically useless.
Top
User avatar
Yodo
Inserter
Inserter
Posts: 24
Joined: Sat Dec 30, 2023 4:27 pm
Contact:
Contact Yodo

Re: Flow Routers - UTU balancers without the balance

Post by Yodo »

I should have phrased it more clearly: I think splitter squares are boring, and these currently seem to be the (physically) smallest flow routers. Making an n-n FR with less splitters than than an n-n TU balancer would be quite useful to make universal balancers smaller. For use in a universal balancer, it is better that a FR have fewer splitters, as there is generally enough space to move them around, while a splitter square is harder to rearrange.
Have you considered using flow routers instead of balancers?
Top
sh4dow
Burner Inserter
Burner Inserter
Posts: 6
Joined: Sun May 26, 2019 8:50 pm
Contact:
Contact sh4dow

Re: Flow Routers - UTU balancers without the balance

Post by sh4dow »

Has anyone done a book of M-N flow routers? I used a 4-6 flow router for the input sides of my universal smelter, and think that there are other use cases where they are important.

Obviously, a 6-6 flow router could be used as a 4-6 or a 6-4 as well, but a design with fewer splitters/priorities might suffice...
Top
Post Reply

Return to “Mechanical Throughput Magic (circuit-free)”