There are three machines. Each has to its upper-left a constant combinator; turning this on/off will start/clear the calculation of that machine. The left two machines calculate π (though by different schemes), the right machine calculates e. More precisely, because Factorio represents signal values as 32-bit signed integers, I calculate 100M times π or e, rather than the quantities themselves.
This very crude "100M based" fixed point representation is then represented in a "light" display below the machines. (The right-side info display displays signal values to most three decimal places.) There are 10 lights per digit place, with the lights having the same layout and meaning as a typical phone (i.e., DTMF layout). The first digit (from the left) is the 100M place, second 10M place, third 1M place, etc., so naturally there are 9 digits in all. Hopefully it's easy enough to interpret: you feed an "X" signal in there somewhere, it's put on the display.
Simple π

The simplest formula for π I know of is 4 * (1 - ⅓ + ⅕ - ⅐ + ⅑ - ...). My combinators worked by iteratively calculating signal "D" that increases by 4 each tick, calculating a pair of positive" and "negative" terms in the sum 400M divided by the appropriate values, subtracting one from the other, then accumulating the result into signal "P."
While it's easy to remember, this sum converges slowly, and has terrible accuracy. Each one of those accumulated substractions involves, inevitably, a catastrophic cancellation. Here we see a portion of the sequence a minute or two in, when it's up to 3.141485 (the animation loops at 3.141488).

Better π
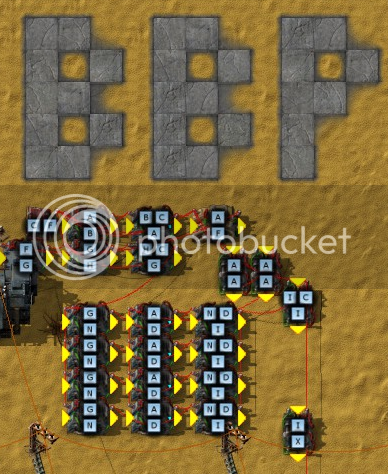
This is based on the BBP formula for π. This is more complicated, but because the summands decrease exponentially with each step, it will converge quite rapidly, with fewer accumulated terms, and so less potential for error.
C=1 and F=100M. The "top" tier is responsible for incrementing A in steps of 8 (A=8, A=16, A=24, A=32, etc.), later used to calculate the monomials. The second tier is responsible for, starting from, 100M, repeatedly dividing this number by 16 in signal G. (So G would first be 100M, then 100M/16, then 100M/16/16, etc.) Then we have the four parts of the sum, G times the appropriate constant, divided by the appropriate monomial. Each of these inverse monomials is accumulated into "I". This one is a little bit tricky because the "I-C => I" accumulates the output "I" every tick, but "I" is only updated every other tick, meaning "I" is double the size it should be (i.e., approximately 2π). So before it's passed off to the display I just divide it by two.
It finishes in the blink of an eye, so no animation here. But this is the result. 3.14159270 is the calculation, not bad compared to 3.14159265. Considering the calculation methods being off by 0.00000005 isn't so bad, I suppose.

Calculate e
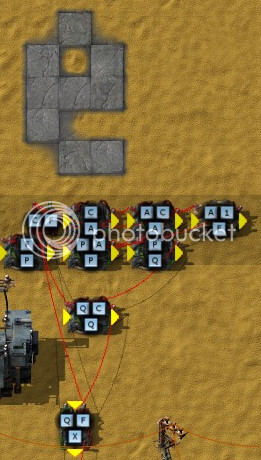
This is the simplest, since e has the simplest form, "1/0! + 1/1! + 1/2! + 1/3! + ...". The terms vanish super-exponentially, but then again, my method of calculation of the inverse factorials will consistently round down on every step. The first tier accumulates an "A" going 1, 2, 3... . The second tier calculates from this A the running inverse factorial "100M / 1!", "100M / 2!", "100M / 3!", etc., into "P". Then this is summed into "e". Because it was awkward to represent "100M / 0!" in the main loop, at the end I just add "100M".
Since the terms vanish so quickly, it also converges in the blink of an eye. 2.71828178 is the calculation, which compared to 2.71828183 is off again by 0.00000005. Not terrible for integer arithmetic.

In case anyone wants to play with these, here is a dropbox link to the relevant 0.13.6 save file. This is useless, but I had fun with it. The appeal of this limited, admittedly. Certainly there may be more clever ways to do this kind of calculation, and more compact ways I imagine.