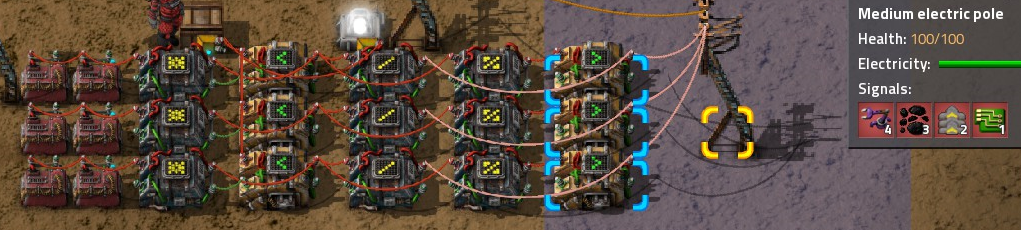
Basically, you want something like this:
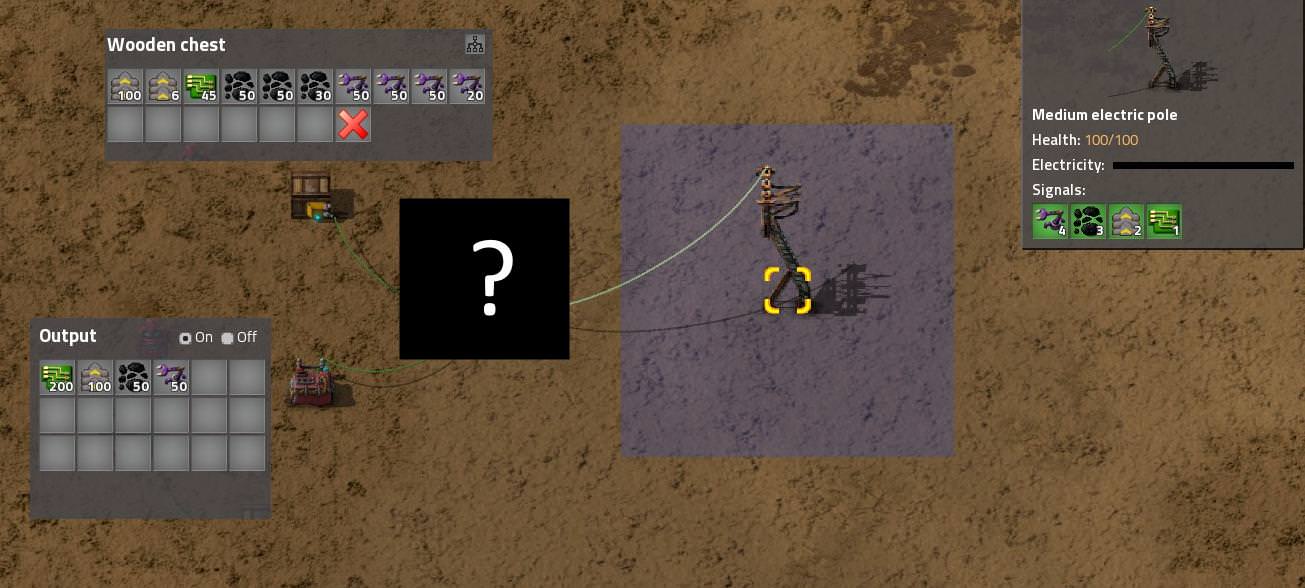
The idea is that you somehow divide each item's signal by the corresponding stack size, but I can't think of a way to make that work.
An alternative would be to have a bunch of arithmetics each with a different inbuilt stack size, problem is the amount of them (would need 7 since there are 8 different stack sizes - 1, 5, 10, 20, 50, 100, 200, 2000) and some kind of signal filter to get each item to a corresponding stack divider arithmetic. No idea how I'd do that either.