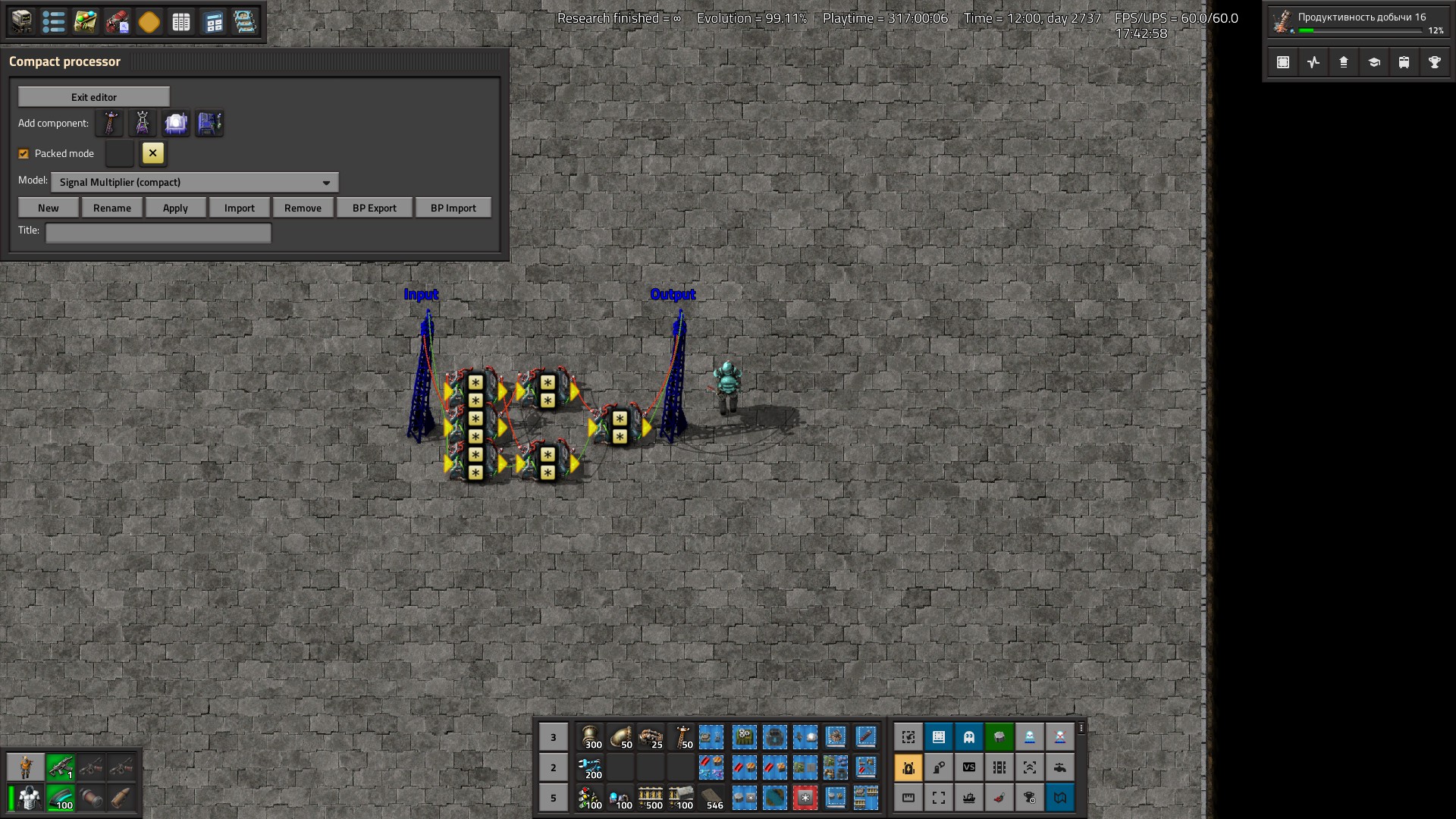
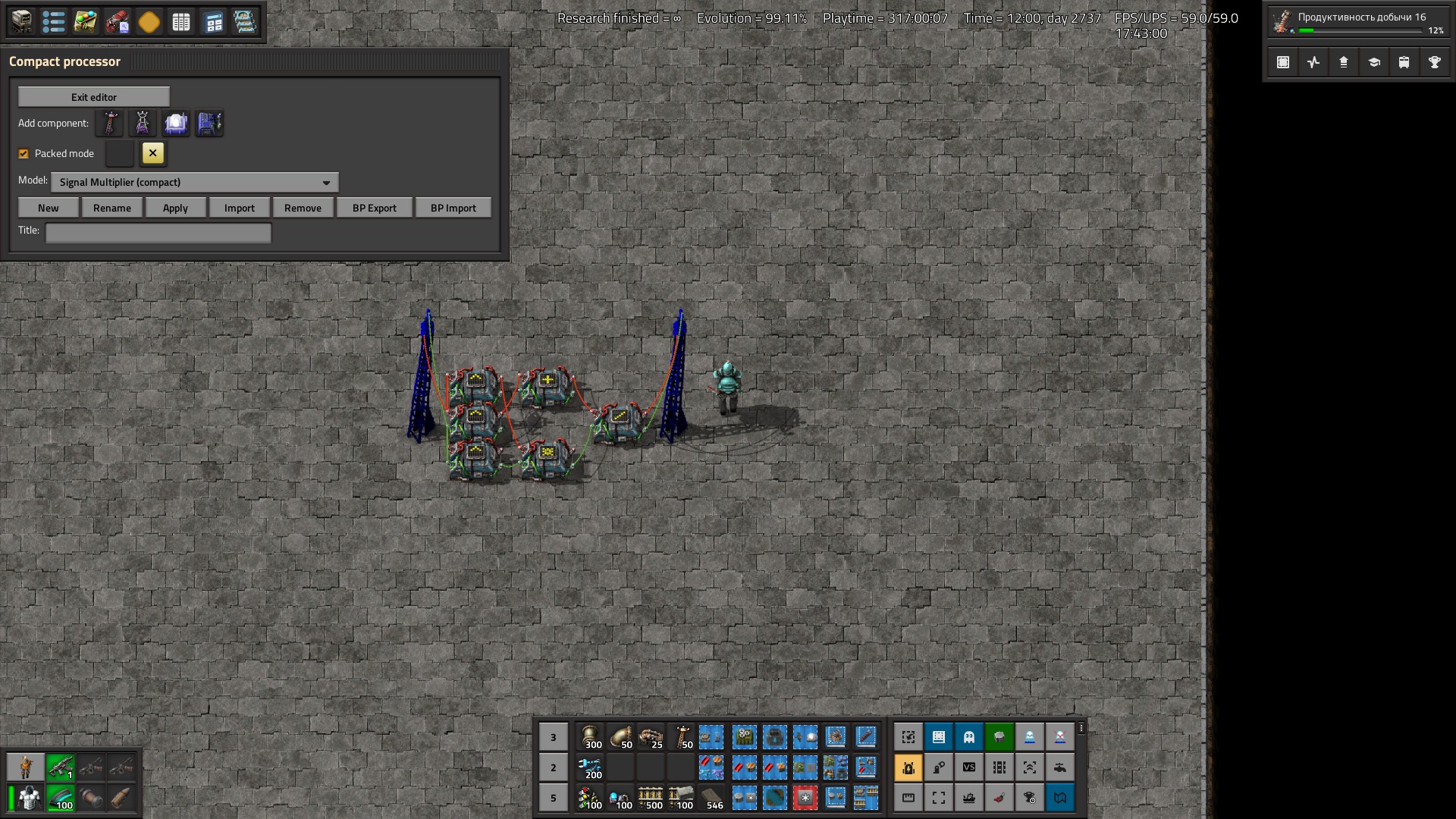
With factorio 2.0 the blueprints here are obsolete as both combinators have gained the ability to do each(red) op each(green) and thus all basic operations take one combinator and one tick. (Except for addition, which can still be done by joining the wires.)
As for the bonus blueprints, both long multiplies and logic right shift will need to be redeveloped, min and max now take two deciders and one tick each, any kind of filtering can be done in a single decider.
=================================
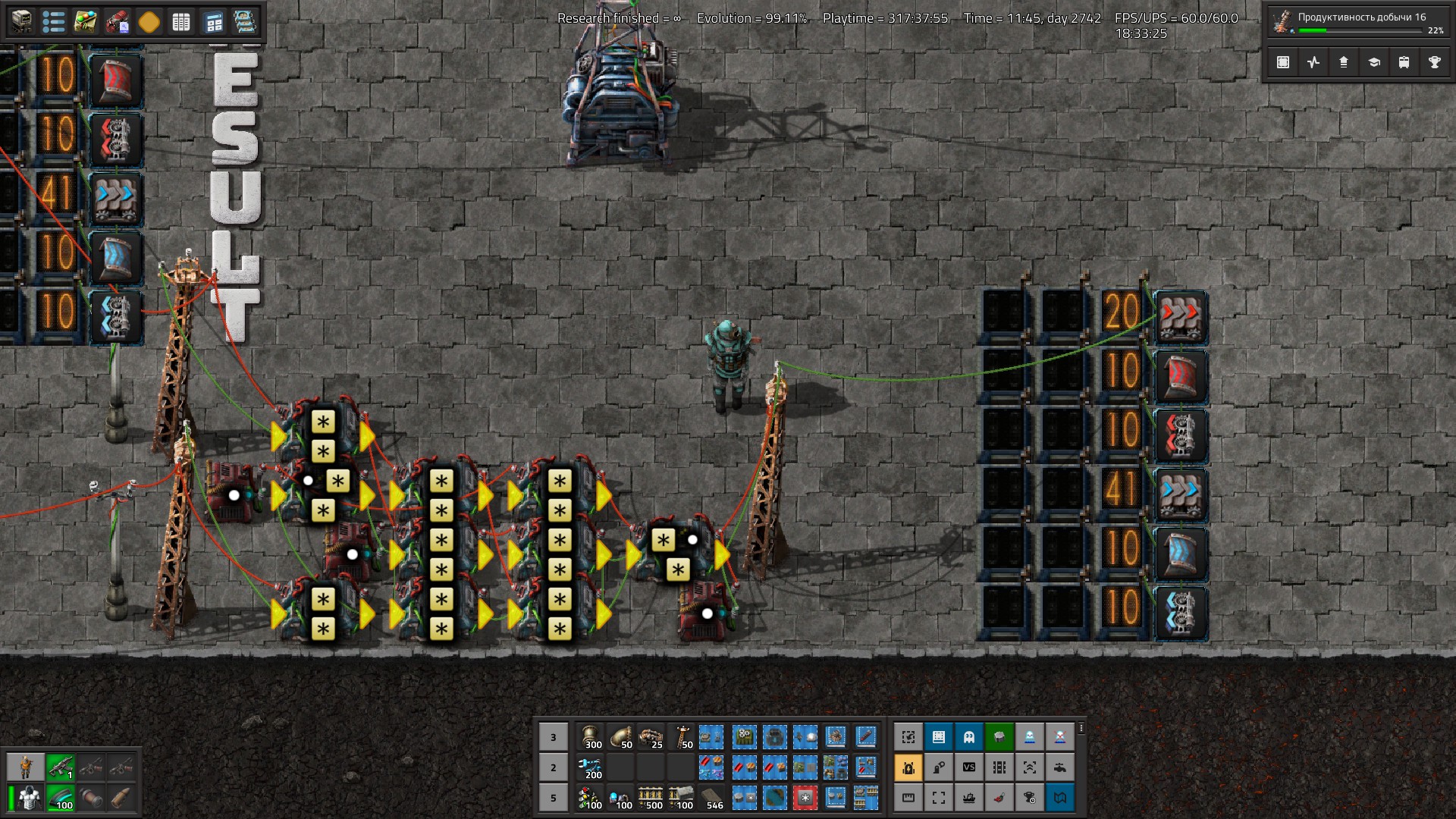
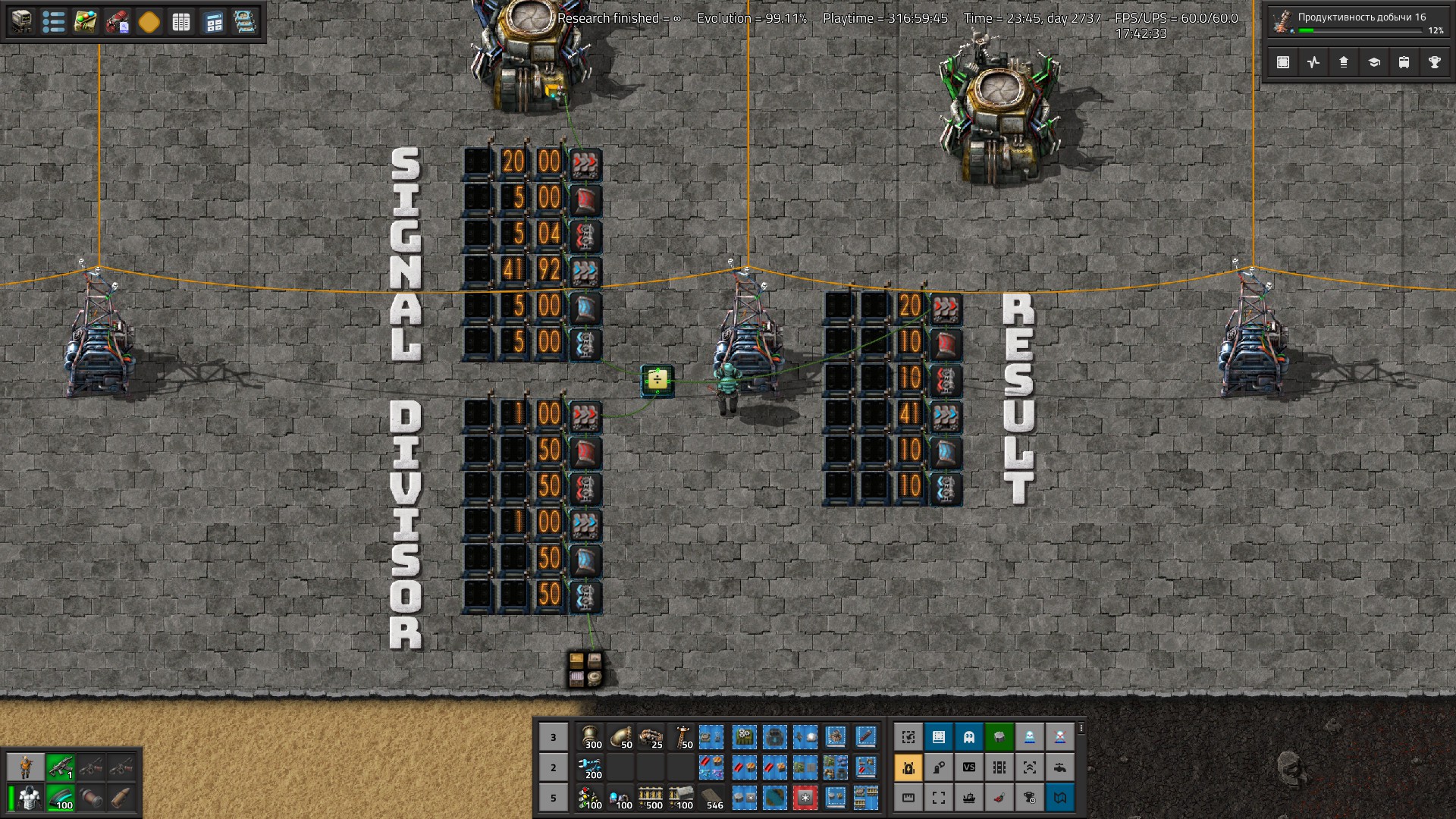
I occasionally search for blueprints for doing a combinator operation on two wires rather than two signals, i.e. both inputs being "each". But aside from the well known multiplier they seem hard to find (or nonexistent). To finally have a full set I decided to make a book with solutions for every combinator operation, whether well known or obvious and tried to design the missing ones.
All blueprints have constant combinators at the top for the input, and a wooden pole at the bottom for the output. Throughput is one tick per operation, i.e. input signals may change each tick.
Improvements welcome!
- + add
Latency: 0
Combinators: 0
The one thing the circuit network does for free, just connect both inputs to the same combinator or wire - - sub
Latency: 1
Combinators: 2
Negate one side, then add - * mul
- Latency: 2
Combinators: 5
Limitations: All powers must fit into 31 bits
The well known rearrangement of the binomial formula (a + b)^2 = a^2 + 2ab + b^2 => a * b = ((a + b)^2 - a^2 - b^2) / 2 - Latency: 3
Combinators: 20
Avoids the inaccuracies in the simple multiplier by putting the division before the exponentiation and processing the lost bits separately
By almania
- Latency: 2
- / div
Latency: 12
Combinators: 113
Limitations: Inaccurate by ±1, depending on inputs
Approximates the multiplicative inverse of the divisor, then multiplies that with the dividend. Special handling needed for dividing by 1 and -1. - % mod
Latency: 15
Combinators: 144
Limitations: Inaccurate by ±1 depending on inputs, inherited from divider
Calculates remainder by dividend - (dividend / divisor) * divisor. Thus also produces the result of the division as an intermediate - ^ pow
No blueprint for this. It's certainly doable, I could chain 31 multipliers with logic to feed them the correct inputs, but that's huge. (around 2100 combinators) - & and
Latency: 3
Combinators: 12
And, or, and xor all use the same concept: Split the inputs into the individual bits, then add them. For and the result must be 2, for xor it must be 1, for or either is fine. So, test for the correct result and set the corresponding bit in the output. Since addition of two bits will at most produce a two bit result, we can split the inputs into even and odd bit positions and handle them in bulk. For and and or we need some special handling for the upper two bits since overflow both from and into the sign bit are awkward to handle.
Split even and odd bits, add each pair, then select, shift and merge the top bits of each addition. Special handling for sign bit - | or
Latency: 3
Combinators: 15
Split even and odd bits, add each pair, then select, shift and merge the results of each addition. Special handling for sign bit - ^ xor
Latency: 2
Combinators: 6
Split even and odd bits, add each pair, then select and merge the low bits of each addition - << sll
Shifting left is the same as multiplying by two. Thus, convert the right side into powers of 2, then use a multiplier.
One version for each multiplier above- Latency: 4
Combinators: 13
Limitations: All powers must fit into 31 bits, inherited from multiplier - Latency: 5
Combinators: 28
- Latency: 4
- >> sar
Shifting right is not quite the same a dividing by two; also, dividing is complicated…- Latency: 5
Combinators: 199
Sort input into groups for each possible shift amount, then do a hardcoded shift - Latency: 7
Combinators: 70
Shift right by shifting left. a >> b = a * 2 ^ (32 - b) / 2^32
- Latency: 5
- < less, > greater, != not equal
Latency: 2
Combinators: 3
In e.g. x86 assembly, comparison is the same as subtraction but ignoring the result; we can do the same in circuits.
Subtract, then do the compare against zero. - = equal
Latency: 3
Combinators: 7
All signals that are present on either wire, except for those that don't sum to zero.
The trick for </>/!= doesn't work, since circuits don't distinguish between zero and not present. - >= less or equal, >= greater or equal
Latency: 3
Combinators: 9
Combines the circuits for equal with less resp. greater than
- * mul (long, unsigned)
Multipliers that also produce the upper half of the result, treating both operands as unsigned- Latency: 5
Combinators: 72
By almania - Latency: 7
Combinators: 66
- Latency: 5
- * mul (long, signed)
Latency: 5
Combinators: 63
Multipliers that also produce the upper half of the result, treating both operands as signed
By almania - >> slr
Latency: 7
Combinators: 62
Shift right by shifting left. a >> b = a * 2 ^ (32 - b) / 2^32.
This is a logic right shift, i.e. the sign bit doesn't "stick" - min and max
Latency: 2
Combinators: 5 for one, 6 for both
Calculates the difference and conditionally adds it to one of the inputs - Filters
- Whitelist (non-zero)
Latency: 2
Combinators: 7
Filters left side, only letting through signals which are present on right side
Author unknown - Blacklist (non-zero)
Latency: 2
Combinators: 6
Filters left side, only letting through signals which are not present on right side
Author unknown - Whitelist (negative)
Latency: 2
Combinators: 6
Filters left side, only letting through signals which are negative on right side
Author unknown - Whitelist (boolean)
Latency: 2
Combinators: 6
Limitations: Values on right side must be boolean (0 or 1)
Filters left side, only letting through signals which are present on right side - Blacklist (boolean)
Latency: 2
Combinators: 5
Limitations: Values on right side must be boolean (0 or 1)
Filters left side, only letting through signals which are not present on right side
- Whitelist (non-zero)
0eNrtvWuSG8e1LjqVuh2x75FktFj5zuQVGSHLb8uSLdm+O4KkFGB3kcQxGugA0KR49tUAPAv/2QM4UzhD8UhuAd1qVANVleurTABFVe5weJtoYNXjW2vlyi/X47/OXk5viuvFZLb6/uV8/o+zx/+1/WR59vhZ5Z/rv10Wy4vF5Ho1mc/OHp99OV4Vs4v3jzP+fPbF/OrlZDZezRfLx5l6PvtycjVZjddfLP/9+XSaXc/fFYtl9tGzyaq4erIoLs/fTRbFi+/4KLv96PWiKGbbD3e/mP1i/3sff8c/zq5ulqvs1WSVlfc4zwTLXk5Wy+ezvy2LZTbOFsV4sRjPXhdXxWyVzV9lqzdF+Y3Z/Goynmav5ourm+k4+2hcin9ZisueZOPyv3+R8fHL9UfrT56WYj7JXpZ/+mj7vfPN987X3/g4e5Txs9HZ5KJ82M07W05ez8bT9Qtbvb8uyje1vvHyG7Px1fpf48Vk9eaqWE0uzi/uX9vZj6WE2WXxw9lj9uOL0Vl5u5PVpLgVuPnH++9nN1cvi0X5BY+o0dn1fDm5Rem/zkqJkttP1ejs/dnjc2Hy8kqX5eu7uP2CHJ2VN75azKffvyzejN9OSgHlr7aSvy//fLmRtlz/4dVksVytP1uuxmutyEdny2L9lYefza+LxfhOUT45+/HHH0d7j8HvH2NV/LC6npbqdL68Gk+n56/n08u6pzD3T6HLB3r4HHp09ra86btrMlVzQQFf0NEvKGsuKOELWvIFuai5oLq/4E9gePSi8kb17vUaNOPVZLoqTZmi6e/m88u1Yl/Mb9ZqISoqPvL++GJe/nH7Y3X/Y0748XI1nxWVX7P7X4sfX2w+ns1un3Oj1Gz9X6WvqVrbpPyXKb85WVzcTFabf5aWWavJGn3t7pivXYW8dnHw175x6Lsv3tJevME9YUXjZQxPuPdG3k4Wq5vyk+1L2XzjvBhfvFm/mj1vyR96y+/KX85vVtc3sOwf6YpddY/rf7v99z06443wsJyGj8XxccPDp/YVazJCNfBS8XEhkcSQ7Wd/YRiRHVkLbIwG2xreALvi/cDtfAe4R8cAbgcP3gic2fsiAFyz2Jpv1kMcFOT3BeJTIOwg4PLdbz/0uqwFyZyI5Hafcxv7F9PyKRYlmtfzadGOozKb6JD45PW6Vd7/Jkh7XNnLj86m45dF+frPnt299/Pb1/2k8tZfZM8u5tP54sn7Yjqdv3vxybNHm3+Xn7f8qJT9toxTb/colknjuLHSCe30doubr98ThVoQO9QCz5/PPn87n1wuNzv58vOLi5vF+KLcKZf/2Hy2nFxdT4ss+oNlL99npeauJrPXm+tcTt5O1o+ZvSxezRfF5rPih+syAC4R2Wh8Np5dZteL+UWxXP70q+l8udpQFNmyuB6XllFM3z+f/fJ9Np5ejWeTcc+JBJf/HIgE645MJFReW6d9PUwkOBbGXKBEgrWRd7RNy0Feu7us39g2yWC1MjgkgzfschEZolaGhGTIWhkKkqFqZWhIhq6VYSAZplaGhWTYev3AFMTVC8E05PN6IZiK/LJeCKYjX9QLwZTkV/VCMC35db0QTE1+Uy/EIsSejsTkWXckv/fbCH7vdxH83u8j+L0/RPB7f4zg976M4Pf+FMHvfRXB791uUbZyzreCHIG43aGMZe4qrHEO3cnXMTzwn2N44L/E8MDfxPDA38bwwH+N4YH/FsMD/73JAyNC1l55K0YrJfRWlINEXc5X9a4tR9aEXU6cysYZcM2oxuZHi5XznsTKPEKsLCLEyjJCrKwixMo6QqxsPGuG19XnrKuzr4bbNka47aKE23mUeDtOwM2jRNwiSsgto8TcihJ015+G7NGr6Dki0cXyU4TlOkZcbmIE5jZGZO4ihOY8jxCb8xjBOecRonMujhWe00KdcxYjSucyRpjOVYw4nesYgTo3MSJ1bmOE6tzFiNVFHiNYF4eK1qFVwETLRrA6cjZC3XEEfAxaPbI4P8aRZ81OhXj87MlHEAfLR7C9z8N6+vQo0HEydBzM0ZJE8PBTQOv6bna/OAZ2/hStBiixXC69++2HV+U5WYM0USM4fi4se2fOYufw+LPPjmLPZDTM7l4oR7SC0/2G9egPcQ/GRNDyzIebLOjIyWESUgHq6iyDVucBA7dmOohG5ssjExCy1KV7m6ZxWVxMLosFPUuDBuud2DiYPljlyxvd5D+tr3PW3TWvBV2//36zL/n+1WJ+9f1kVoo5e/xqPF0WCNay3U3WLJ7AMtsWqHFFRFsHBWq9yfpl0khbhgn2oUV//c0ptkp7hqq6bqUIktqiPEPMJjUhOXu9V4LPv/rVccormA2JwXex5rprNLYnieoM8NKa6rljT/RgzUcdeM9N2kvv2a4B99pU63XYgl09x0gL9jPfvrd9mSUWc3KczHIiLbPg4uhCNrtN5sU7JLSrITrFIEKBg0QkGb0w2mmIoQ2BUN4LMFhXwpkgqc2GPTtkbsn65/EtZEcfRmjlAz5vEkiN3S6b0cx/1XyzHrkwRisf7pEFkxByAtustCCLS6pHHmW8HAr7gQLoB8vCg1D6SfxQerW4KbD9kML2Q6jBt++WEYfglVSvNhrcd+U9UZvdfdfT4yoLkahqUQWFrdV7f3fNuhFBdL2yGFBZRPIxFB/jPHhwSLE0Fk62+BhcUr3aWFBtZPIxwH6/RRUMGWoiTccd2LKhsl4ohbRsAJZC/aE0d2DU5g5st3EkY2KndeTv7xo8rIp1+4X/87/ZKLssrotS/2evs/ks2+jX8vns8+vrxfyHyVX5xdvOEFc309Xkejq5KCW9XTeKWN93se4AuddGcrT+wez+FxsB41X2rgz/s50ulJ9m316XRjieZm/Gs8vp+iZmRXFZXK5bSW46QmxurLxVtmn+cM763c9B863iWnX0fg6P4vRz0Gwb5VtRk+5f6XagI7RzePDWPNdjLEI7B80Z+YI8QjuHBy+UpRK14ZWo1ZeXmYBShfvYVIVUq7H8p/+Dypt3mlqe14gB6ye+bKjC4J0LVM5518qHaoXKueha+VCtCDmXXSsfqhUh56pr5UO1luPc+CofHmK9GL87fzVZvkFqlD1dTGu0haJ1k8V8dj5fFB7Nw6qUD9OS9sEKkzx+8vgxPb4O9fghvp4lJz8MJ38e6OXPWTQHT3HtR217XQ3ojRvu8ZeK0jUZI/qqSyvx3X+4SVwg0UeumArrhs06FmZxb6EqTQF4TxXg9EyvPUwfbd5RLKVsI04B7AOPbIbrkbE22+pQJa0PnPSA4bAQHL4s6oPVmz5wqWa4iVgusEl9pEJPzcXwrIcaQLQAYuECTlK8wSrTvlSKN7oXZQGl9cT8NbBi80GUoNLeASrYzCFbJG9FmC8nTR6qnPNBkBL5tPZB7lAMh/uoF2UmBjJ36vgdExSv9B25/zgKcjqw20WkqsgHoYsacGK4CEkMZ/56xy77YjHgEgsF4ZFHKonpwGPYvuPVw8IK5g5V0PggRhgyHroRD2KRorfC31fECHPDok8B/r//+a8eNGUxIIpEioN3oDhUsqva/hVtfk7Qi4o9XcoE8WwOLw3UXA4PWTKJ0RJzOCIiCo8pKoiwfpR1r9eTExTlQ/tXodptSAvP36lRog6KEoeDaKfydcGw9grCBqJOPFTjYaxHT1Bfd65WJ2nMwD3WyaCzA8lQVB/+3RC5Lo4muygU8kMVQ7LD10C2hrPEOvhWh57D9Wpdgh423HCWQ9t26XGlhkiLiRw0KtMTo/oZ2BT3pPwY4nIoOlAzeqjLIami1RfoSF946wmEDHELKTqko9jkTWFLlERKTeBkDau0ZHA92W6cJOgUUL6DNB4L8vzdUtc/nKRhqneInqIjOYgnMcFIoFkpEgXjQPGI1EKyPeL6v09PXAtPpCg8yStcYcS3JJJxogN1Y4boS4lUSzsqKg/0p9SIJaggaDD+FMW0roCISJsI2zllM3nUJqQ8g5CEx5q4RqJTRUw5Ei7kiH7Y0amEOsgqgXrLnb8T9xsyD0kiG3J0CuJJTJSVrHNKRfKl9dGpa7cU6bEkDqZlKCKnJnlIWsbQo1OpwOhUo7v5jv5UhJxO6AGXq3PoSFARj+9lhxQZk3YLPhurQ4TIv0iQf6kcJKQVrgkp7lnjPAyMYJDtEfkXqUPOFobsCwXUE1YTmRNpgs4WTC8jjuPkpglBbV0roW4d0nWV25QeIW3QcYPpy2CZExTYCSw/Ij50LiR5tC/Q7U50OsAo6vq37GHEBJTwKz0N9aUns8KRq6mDr0Q8h1R50GnIkL2/Imf2iyDatdmFKOJYMcWCDkcG7f3NiaHjIYnmA/L+dWh4ODwBFfIoT4Gp8iS1O3ILtuArESN/JYLObQYd+ZPDPIXRJaqr3EYHIoOOcobs+yXUPuUA0KmQcpOhR/6+s1KJsVue6X3K0xLHkcejB1+JmJ+hdNBJ06Ajf3KnJMlDKNQWF0IkD5QJOngacBtICSVyO+LxrrJBB0+DXo3liU3JhVS7DHwn5jlnlxALpzzjChXOjY1o+QHwlYj5AToPOhMbspuGqDVHPKPUHQizys5Y9cVNV9rinSC3UZMJ0ppvtp1sErkz3YE7471D8TQeWzO0pUIjtrikNuw93Jf27J4MMR9Fh1XcqQHvjjSHC3vIbiEknZ3sNsJK85Lzv33bZMJDQ31QNXHevVZBB5tDNmDf2Hg6tL7B4geCvkOFn07r/u07lnCrpCazxiW1Ye9hPbVq/7slsqI6rI4wOf+GJX4HLfrUKyhxThO5HG2DTj4HHd2RoRMMVoIY0LqQCfADd/4GbS/TaLa4pDbsfQGJh4azxDI7kwcdiQ3ZLRgWyy0YqILSENsdGxZ0EDZot2DwWsgG7Ov6T7Vg68mDssRqL8ODDt36HtN9/c1RlACi6YwvHKeO+RXdy8J+7sOi0JLn/VLKHcfLseJZL8bEwxbTIUOth1uuHdf8yVGMUoVC1gCJCjqPHPZqKbE2/u2ktSFnlBvfyYckYq+Dzj7FcHt/GGhTYywZWUtELqySUwy5zINcySnAqTpk8NB2WRxFbjBjMbVnkJGBTh2MjlXTZwx2X13rOowLOsAcsAe3EPdgGdVpWCJLYcOqMQftwd2hPDgZPLBJV/XMMXnwh57Q051LQ4kfxsWqzPNJsnmc2gzLg04hh+zBJeTBJdmDE3dPNqymMsXgpNYZHPTgVPAkyDbmyYM3WZYndU9Dfd0sj5XR75NkRZy+GlYFld0O2YNDA/8s+eyp5pv1yIXVRaYY/CAenAqeAT24TB68ybLA8XkeD65i1Uf7JFkdpybL2s4TyvqlSk9Pv51Drd23YSMe/FvX/fT4pBA+OOs/9Li5NjCJJ00eOH1VksRkAJcH1XMNeCqZ8SBA71rok6SghgfOE42znEh5OxaU8j9g1bAMBpRMco+8bW9aVEPQIj4XRpUNerY6fdvsoOwv56NBiXyME0G53IOft+08JIz1FNWogGa2o8A7adUvhoX4+8sKkYd3KCEoUO0bTvohfYfnoPN5RyzrdWHd1AYcIiioByrLiWPDnA5KyR/2yu1JMrQGjsWajDH0Su4gUZ/pTs6wAZMzxP15u30Tj0Cc7c6+sAFzsURKrB0jYsWbc0GJ3gNeFHWOAUJsELhhPLqTXKqfA+COk3nvcoyX3NsG8EZQWMhGtDegqD6QDH5Uct/uTfq+YKjGxjvP1VQu7e9aW6D6HKKlYiRCqjfVgOeFOYNanqT6QxnSC7WnmJwfBRMbvEaN2sPxZtDQEYs2OTtGbCQazdnpkHEvygzEsBpMBcocY4xRQTEhOb1qKN15G0DxtH6uDcJbPSLjVNxs9+jOnNLhscMnfaAOb4/V3V+HsPiPecZzMCapMINZPpWKKZV6RBCcYrs1UvdaLA85qFeD7ilQYy3Q0rZnrExTUWNBAUnqnXPrG51vEdSY88yJMT/jQaHLENtZ0mLLfYtSqOOk7glYUBZMXzC8h9CcoE/OnsHsGyC6L6eve0ED+Hpvgv95LBeKHVIycptSwBCDMkj6bojH86WMY8GMo+KjwY1AJbxMFRv+CKMNI+/ySO521ElWg0KAWSLVyDXVf7QEQ86HkMC0R9OVQ1OxR8kflrDv4ry5j7eBsR+1u/+9L/AcUZcu0hs0zHWnF9Ny0757CtYqYLmhriZ8S2Atr8bT8h1My0dblCHg9XxatO/CpPlUIa8j9PbLr09WxVV5qy+nN8X1YlLiPjqbjl8WJbhnz+5QPb8F80kF0xfZs4v5dL548r6YTufvXjx69mjz7/Lzlh+Vst8Wi+Xm2bkt/ZfjxkontNPlU09ml8UPd5hub2ej38uLxeT6LgD9crwqZhfvH2f589kX94a03Pz7r2+KbD4rstWbyex1+d9FdvfM2axYvZsv/pFdzotl9mq+yF6Vr2mU/c+b5Sq7e93Zy/nqTbbRzGW2mm9+viyBzLbmmpX/eVfaY/kgk4sNOuVr3jOGzSu9V4ISuPPNb7aPuNllbNCZFMsqVPdKhO4gZEWJTH6ok6QHnz08Jaq1hS2rtCp+WF1PS+TOb23i9Xx6WfMU1ZIr++nOTqj00W/Lm767pqi5nkCvVy0D8lxP11xPwtdjQdfbbix/QqJdKaqvU39K21i+mkxXpY1SNPvdfH5569xvNpx3Rb9H3h9fzMs/bn+sHtq/58fLVWnllV+z+1+LjcOn1rs21682jQ0BEagCfngEVAgC4sNAwGCr6wMT58jqqnZbETWP/93/Zsy19Rfx1lZBXVvZztrKn8++Kl6Xf82erR/qyeY9bJa1F6P1QjnLxpeXyKpYv64ddomUp1wizyMtkdXaQc8SwlmUNVLSLyiiLJKKfEEZYZGsvtC0SNa4aOJEPPS1q7Qyemp5iG2ccUdY0XjZj9OG/BT1qu0lhs2ljk1thHAgVGQgPtScTB0ZCocGibKSw4wEiZ4zCPrsBlROzADzPF6AKckBptqJMJmUz2dfTq4mq43ulZ/8fja+uLhZrIPOl++z//O/WXZZXBel0s9eZ/PZHVEzKv//m6K0iuIyWzOLWXTSqrzP8fTiZh23LLNFcTVeP+pifUu3ofBP/M6L7Dz7aPejR/vx8sfZJ/sffpr99c3NMhtPl/PsejG/vLkoLxb9UbJxeYn1mytX0avisoyiin7H7FVuVLCjx+yP4sTs1RNk7mpiHQ/tg4bs1bfmux5jEUL26qmY74I8Qsz+4IWaGMFj01qWVwK53BNDNslgtcEgh2Twigz+cDtPliFqQ1oJyZAVGfJehoJkqNq4XEMyTEWGuZdhIBmX81X1rf50nLq9JUuI9nf2GSz/6f/upTh8w3FeI4bl0MN9+UDcVgqmdn+qStnqHcMU76uqlMoGGFO9r6tStrrHMOX7c1VKZVeIqd83VSlb/WOGgPVi/O781WT5ptYrMNtlh1mjLRStmyzms/P5ovBo3uZo+8R0wYMVJnn85PFjenwd6vFDfD1LTn4YTv480Mufs2gOnuLaj0pJPgjo1YBb6Hnqw4n9zDunNHKVhhs84Bep1QF6t7UolrpObnlJbHvXOeOwXwpw+oxDSx43AQHOO4rdy3cU1OLnII8sBtwSH8onpdais5ByyyHDgVV3+XLQqdXNPKSgq6dwHaeNEZaNTcywFiGVkoOxHmoA0QIIteJRdi6o4ywFnG0h/p7LUlCcQa9u9RRWcOrKpjqX0nGWQk9fMNEMNSePl2fU7n06KEiJfFr7oNwthsN9dJyGAh5zhlqRcWonMhMUr/Qduf84CnLQcAlO7TVmg0KXAffRxkqFOXVf7EL2xWzADUqxQkvuCWs48dSQ5yFtptiAm/wyrO0ekWjkQUTGoPHQWCMh7uEyOJHL4N1bmbNedff99z//1YM+iGDrbE6kOLgIGS4+aLuCGEJBJuK5be8MJohnc1yGTLMaDLLknWtLzEHsB8Xxdl2sgogZ8nwxDu1fhWdUvPZMf9TUKDGoO/qAECWuUTueDmz9K2wg6sSRSDyI9egL6qebAss91smgswPJUFQf/t0QuS6OJrsoFPJD9e86dff2euOHaBZB7C/MXVDQY4YbznIo5JGeZvmGSIuJvPPYTDboiQgRbIp7Un4McTkULGT20sCWw3rcNBboSF946wmEDHELKXjIMM5Be1PIEiWRUhM4WcO2hzpM9XIU55GCTgHlM0jjsSDP3y11/cNJGqZ6hyh/iOh3PcSTmGAk0KwSiYJxoHhEaiHZHnH936cnroUnUhSece5cYcS3JJJxogN1Y4boS4lUSzsqKg/0p9SIJaggaDD+FMW0roCISJsI2zlPL3nUJqQ8IwyFx5o4NNxJEVOOhAs6oh90dCoZZHsC9ZY7fyfuN2QekkQ25OgUxJOY8yxZ95SK5Etro1PPHDzpsSQOpmUoIqcmeVBaxsCjUwmOvlMa3c139Kci6HRiwOXqHDoSVMTje9khRcak3YLPxuoQIfIvEuRfqgcJaYVrQMqT9iA9DIxgkO0R+Repg84WBuwLBUfw0ETmRJqgswXRy4jjOLlpQlCb70qoW4d0XeU2pUdIG3TcIPoy+vUEBXYCy4+ID50LSh4Vg5lWX/+WPYyYgIpWpKeJtvRkVjhyCW3wlYjnkCoPOg0ZsvdX5Mx+EUS7NruQmm/Wg8yCDkcG7f3NiaHjQYnmw/H+dWh4ODwBFfIoT4Gp8iS1O3ILtuArESN/JYLObQYd+ZPDPIXRJaqr3EYHIoOOcobs+yU0ef4A0KmgcpOBR/6+s1KJsVvC45OlxydrsvcPvRIxP0PpoJOmQUf+5KZXkodQqC0uhEgeKBN08DTgNpASSuR2xONdZYMOnga9GssTm5ILqnYZ9k7Mc84uIRZOac8KiXNjI1p+AHwlYn6AzoPOxIbspiFqzRHPKHUHwqyyM2Z9cdOVtngnyG3UZDur+WbbyaageWzNg0422YAjXO5p1kqHlmtYUgzoOxTM8d5Bf5rFWjO0m0ajWeOS2rD30J7a07/MEFORdFhpXnL+t2iQCQ8N9UHVmugBVNDB5qCdv+fsmQ6t1/kfBvoOFX46Of/bdyzhVklNZo1LasPew3pqT8BiiayoDqsjTM6fFj7Sp15BiXOayOVoG3TyOeTFgQ6dYLASxIDWhUyAH7jzN2h7mUazxSW1Ye8LSDw0nCWW2Zk86EhsyG7BsFhuwUAVlIbY7tiwoIOwQbsFg9dCNmBf13+qBVtPHpQlVnsZHnTo1veY7utvjqIEEE9nfOE4dcyv6F4W9nOf+4WWPBtPOVhLqWW9MfswJh62mA4Zaj3ccu245k+OYpRgvbMhZp4ZFXQeOezVUmJt/NtPLA05o9x48sYMcSib0SFnn7kbbu8PA21qjCUja4nIBVVy9gW505R5kCs5BThVhwwe2i6Lo8gNZsKp8WQbaSi1z+hYNX0+ScbEqeswLuQAc8ge3ELcg2VUp2GJLIUNqsYctgd3h/LgZPDAJl2VM8fkwXc8pac7l4ay/oyLVZnnk2TzOLUZloecQg7ag0Mjra0ke3Di7skG1VSmGJzWOoODHpwKngTZxjx58CbL8o3cgvq6WR4ro98nyYo4fTWsCim7HbQHhwb+WfLZU80365ELqotMMfhhPDgVPAN6cJk8eJNlgePzPB5cxaqP9kmyOk5NlrWdJ5T1S5Wenn47h1q7b8NGPPi3rvPp8WkhfHDWf+hxc21gEk+aPHD6qiSJyQAuDynqyQc8lcx4EKB3LfRJUlDDA+eJxllOpLwdC0n5H7JqWAYDSia5R962Ny2qQaz0c2FU2aBnq9O3zQ7K/nI+GpTIxzgRksudD37etvOQMNZTVKMCmtmOAu+kVb8YFuLvLyvEyUYOJQQFqn3DST+k7/AcVBXoiJ00XVA3tSGHCArqgcpyT9U3y4kcqtMhOfsDX9o9WYjWwMFak7WGXskdJCw03dkbM2D2hriBb3cAxGZoznanZ8yAyVoiZ9aOEZEFdS4kE3zIq6bOMUCkb9Ukkp4bziSAJuvnCLnj5O67HGM29zYSvBEUFpSTOeCpR05hdmSpZsKDyIW+mInqA3Hkt5PctyP3bdlZTsVVdJ6Vmqu0Zw+xPcaoGMmgHIshe0MszGOciogKqZEeNCIG9YWaGjPokI7DPcXk/CiY2OA4btS+p20GDSUebFp+Yjk78vITNA0xH3C75T1y1weJoELiQuZc9RSS8+NMOqmNjdtAIXI/G7kBxQxDsZOGJcX5CB0wK44xKgPEWPctkDjlGsQOn+2GrkF7p1XcR8z5XKL16AVzVJh50C5q0MsYlG/AODWyYCIosmBDhgQ7ZOLUnS0DcziqBdWphRQhdGhds7ikwqSC8vgG3XKoZk2BAsC9JY1Tw3amg8L21FqvNlTcJ78lhi+VrGAmKMAfYrdr2g5s36Jy1HEqqgnaoHOsnmB4D6E5QRu9PYPZj8kZuFejr3suqFC47yb4n0dyoQzjpTg5GZVuiDwPSjDtuSEe0ZdCBeB1UDbgw4K2y0PemzGOWReVqOI8YLvMnRsyJAKDhJoWw8H0ie0mjIrHYMqea+PwNoykL4j0lL4zwejLGn6xJo1BCRbbE43pd5X13qZvf1cIMmbk/kp1X23AXoEnDSxh3yUG4r5DAhj7UXsUte9aIHXpIr1Bw3TXs6y0Hu3hlEfWKkX3KOTVxARE6X0NCY+S9LR3SuUlKQSV5uU2KE4fcBXI3jmVx6QElTfiLqBVcCRIojeYO0D2Ol3z202FyjKIPKATSV9N5Tj+S0Ddt5mgEnOCBRwtDtx7+SI7gaWeCV/yi6TvYAWV0hBblml5NZ6W72FaPvui1IHr+bRoPR/hrrRN5H0dICISIqAMvjeefq0oBz4Zb3jPvq0Uh+aQMinpGupLAZTU1V7IoABMDdmFYSyJJK8qKmihV8Pt8MtqRmCNgLirDT1ymKaDwudBo2foDtB3rs4xwkFSD5aE6c5Jpyocrw2OvJEYErS1brwkOcqzQVG+SqlodXuw/YAfsP4OslqtP6dGzC4gra03qiBYT8iRPdwkmsxGRk7mAcls/Tfi4yXRCBe0L9+H3HXe9ezLorp0yQJy45JLp7phyYM2wM3GzLsf3aUg7JmXGGv3uYraMEWKoBO34ayWgWyQlOiqSTY0GcQQDnHVrHWU3rhH0BfBDrJana7PiSs6cS5990Z3HSqIlhxyBarAKlClJlNmktpfRuogBlMM+ahSBZHK+97A0OHtIKsBfxPEgQ7aenWg9Xq2RJB5+2U14G+7p3qLlLwJsB0e3gtkvb2b8zbt6SCrQXtc12GpJ9aeHiZmSqxXsLRgALf/hTYViSK9XmlU3nWgRnI5rS7H179OguGmA7cbbfrUQVaD9rCu0z2Ty6GQCy0KoehH9opK9quAvCxrobwsZIWsXQDLr09WxVV5qy+nN8X1YlLCOjqbjl8WJXZnz+5AO7/F6kkFshfZs4v5dL548r6YTufvXvzHs0ebf5eft/yolP22WCw3z85t6XocN1Y6oZ0un3oyuyzK96HWL3V7Oxv1XV4sJtd3ofCX41Uxu3j/OJPPZ1/c28nyccbE89mXk6vJahM0lx98Pp1m1/N35RWzj56tn/NJ+RLP35Xm8uI7PspuP9q8ru2Hu1/MfrH/vY+/4x9nVzfLVfZqssrKm5xngmUvJ6vlqPzXm6LcGxSX2VqNM+AVfkJ6hetnnpUvcbV/W7d3snngbP4qKx9m9aaYZTfLIv5tlEhOLjbqWerZnrFvdMqzC9sCvuF0Nro6KZZVxb03KXRDJ822At3kh9rQPfhsJwmw1jVsHcOq+GF1PS0V+fzWRbyeTy/rHmPblUTfeoa35X3eXYazmksI+BK85RJM1lxCwpcQ6CW2/NtP79gD97bzh77NbPUD/moyXZWeoV6Bm1ar/Hapurnr6nevwCNABquVwSEZvFaGgGSIWhkSkiFrZShIhqqVoSEZulaGgWSYWhkWkmHr9QNTEFcvBNOQz+uFYCryy3ohmI58US8EU5Jf1QvBtOTX9UIwNflNvRC7CTSpQ3QaYkeN+j12JL/32wh+73cR/N7vI/i9P0Twe3+M4Pe+jOD3/hTB730Vwe99HcPv/TmG3/tLDL/3TQy/920Mv/fXGH7vbzH83t8j+D21O9GWdiBrULcoThAO5j0JB3mEcFBECAdlhHBQRQgHdYRw0EQIB22McNBFCQfzKPFgnICQR4kIRZSQUEaJCRXFOdYPu9xrXEHzjxb1j/IUYaOOETeaGIGjjRE5ugihI88jxI48RvDIeYTokYsI4SOXMeJHrmIEkFzHiCC5iRFCchsjhuQuRhAp8hhRpGCdPaVpmuuLM8WVLbTsR8ZofoqxvnvjP8h5l2CrBOrkJOhM9AGNLft0Jvrvf/6rBxPHqGBi5TXkXt64VYrIVvlgGE+MhLwjjUDgVOTMXg0ympZP7dAEGqZMhtnWS5XsZrEuQuSGAUELJh/ugolV+FML/GXISfdg4CAZiLdNILVRkQpavQZsIiwHEfF1BvaliFMnzGkcURkZ0Q+1F+eBbMwELUP5kNvWeGwCbExCHglog1aqISNG7zQC7cY4tbrRBa1nQ0GO6M/I1laHGNHW8Ak8VVtTtpeIPTqKrUFN8rinGJk3p1dTflqPbRA30hdsz08CLj35HSpM4+SaAE4sCeBgRcAD8xVIRUDovYfXA6x/9+Kzz+KVA2hqOYDaKQfgNuXKE/yJyu3PIVde5ebQufLVN3WgXHmVuwPnyqtcp1z5lCufcuVTrvygcuUfrA8pVz7lyqdc+ZQrn3LlHwScKVc+5cqnXPmUK59y5bf+keUpVz7lyqdc+ZQrP/hc+Qdb6JQr/6Hmyj+gsVNK7pFy5eWhcuUf7OBSrvxRcuXVQXLlH8SayTA//Fz5BwtmypUn5sq7Q+XKP/CUKS87IIsXy8smZyaqkNyFVP0QlmsfK1f+wSqWcuXjI2JwK5GR83c/UETcgTKvD5Yzr3LV98zr4wyk4uQtNgeHOHJ+qLT5B9FfPuSpIp7wgV4QAQ1W5bJ9vi8nX5fLQyXqK9a/ohiRn2T3Th+2LGMWYQi6Z/HMixbEMJezkAW8p+UcJymdasluh2Z/CmohDg9ZwIeMHKePGPSMaeEQtyOIqzsXIIWuUViHM9N13/ZGvtUUWHfbYjlBPDDhMiSW60/R1WkHMHvm3wAmj0tqC/uINec8iG3qvRIcbSY71yFB+S7WQnYNx/YkUZ2BDuGR+6IHR5gTTSwjHLVao3c7TrVenAVjLLlw0PEG7aQaobOdT0VTrLVrLgaMkIgn1xxnu5gYolMMYhQEyFVSLUwE8VCDDG1ItfQ73tF15aQJktpCKM+sW6HJ9+Xx/1RvIcIYLT3cIynOkNQIwan8V80365ELY7T0cE81OIeQY9hmpQVZXFI98ijjZVDYBzmymAtsP4QafPtuGXEIXkn1aiM75xqfVm36N6sYVAWBrdV7fzfNuhFBdL2yKHCnx5KPofgYzxGJyCHFklg42eJjcEn1aqNBteHJxwCcTIsqKDLURJpOGKzz2YP1giGdz4ClUH4gnc9M185nzLnns2/ni/Vs8lJrbnudvV7Mb66X2av5IlvfQla++eXk5bTIlm8mr1bZ+Gqta3dt0C7n2Th7M15cXswvi8vbb/R94nclPuVH72L29Gmsid+Vx8h3+3+JKAO/dcsVavuk4QO/bdsl8hgDv7f0gbSnaGKGNDBqXxWJ5Q4depbrxjekf7Z1YY0VsM2rnoo1ddSeQCdTJ5XUSSV1UkmdVAI6qXjSWq2/2j3OUFJ3JPeZGq2kRiup0UpqtNLnoaTbPZrUwy1UVnHq9juMz7C9e/+7uSxHy+80sZphsJApJlKmpBRPq5Kab0sDNyrpMIWkL9jcQ2NOAw1rD6SZBrvMEE/yu8zwlB+OYR2rgYIMNKym4gbPwbuvmlG6w40OVf3Tgp1V7pMjgS88pqsOZLoKHKZsUMQOdNLJDn8s3poKTequ5zM15i9Eb0VZ5YebN6p7Z5q9aBw1CgmGLBEuAxql64lR8l4apfIYHTigVHG42QoJRct6gqLoJYrGg6IDUZRw1xUaiqInKMpeomg9ldlgPYrScF8UGoqqJyiqXqLoPCgyEEUL9y2hodiXYFX3EcV9WxtRO5jUn+LlcA8TGop9iW5ML1H0cD4trQvqURQH6VciXV+iG9tLFPGOJe0oSrgPCQ3FvkQ3rpcoekgctBWBpkY3IInj+hLdsLyXMPra9oE0urZwHxAajL3h4npJxnEFd19shdFQ4xuQvXF9iW9YL+kbX9NDDtI3htqQDWwSkvclwGG95G+4h7/hIH9jJNxHhAZjXyIc1ksCh1u8BWkrjMT8AIFOGOpNiNNLBod7GBwBMjjGwX060Jr/E8PYSwpHeCgcAVI4lhjiCHCsUN6bEKeXHI7wcDgC5HAsMcRBO3Cw3oQ4vSRxhIfEESCJY6nNj8COGKw3IU4vWRzhYXEEyOJYaoiD9qroS4jDe8niCA+LI0AWxxJZHLh3RF9CHN5LFkd4WBwBsjiOGuIYEMbe5OD0ksURvtEVIIvjqCEOyOLwvoQ4vJcsjvCwOAJkcRw1xAFZHN6XEIf3ksURHhZHgiyOI4Y4EmRxeG9CnF6yOMLD4kiQxXFEFkeCLA7vTYjTSxZHelgciQ6HzonThCRI4/DexDi9pHGkh8aRAsWRmIsjQR5H9CbI6SWPIz08jpQojsSzKgkSOaI3UU4viRzpIXIkWlOVU8MckMkRfQlzRC+ZHOlhciRa1ppT4xyQyhF9iXNEL6kc2N6ojX4kWi9V8Zs8dfmlFZPvlb4JpLGrdLR6VGmDioh5mqpUU+e/C52CJlgyRg1fwFKpag8APuCuyeQCbno3gD1jZcSthMpD+t72xf52W9Ucq80n8/SpV+gOkGp6CqyMqlZ38zTRzFul3Q4SMU1fdehx45JtNY7e3rEtOLoknj0oEdS9i/esNZE+SXMblWMhB9Wk8J4z1TL7oZuUZ4yHMqhJEQkSpXDY8mRS/j4UbSZFzF9ReK8YK5JJEQfaKoeaFJGrUgaHjSeT8jcFaTEpTuSnFE5qWJVMiji7VIOn3IwTc4cU3jbXymRS/g4tbSZFPLrWOE9hE0/RPPR1x6TQjANOpJc03oLX6mRS/nY5bSZF5JA0Tk/YtM8lNMFpw4bIQWicg7CJOmqelLzj7lDqiBPpCY3TEy7RE9RJxhqlJziRntA4PeESPUFoJNXmCYn0hMbpCZfoiabWNnsmhdITnDo8EKcnXKInCF29WkxKEOkJjdMTLtETzUPUH5qUQekJQd0C4/SES/QEocVam0kRqSOD0xMu0RNNLZ/2TApNoxBEesLg9IRL9ASh3V2bSRHpCYPTEy5tgZvab+2ZFDxfhMhcGJy5cIlVIrQebDMpIj1hYHriQZe7oZuUJ3vCwNO2iFtgo3DYEj1BaAPZZlJE6shoHJu0zyX0dmzBRhL3ucbg2CTqqKll4J67Q9NmBZE6MhaHLe1zCX0220yKyEEYh2OTqKOm9o27JmVR6kgS6Qmb47AleqKpXeMebCg9IYn0hGU4bImeILSqbfOERHrCchybRE80tc7cMym05YIkboGtwGFL9AShbXCbSRGpI4vTEyztcwm9gNuwIe5zLc5BsEQdNbWY3XN3KHVEnSxrcXqCJXqC0Je5zaSI+1yL0xMs0RNN7X73TArNbKHO1rY4PcHSFripve8ubA7dAisic2Fx5oIlVonQ2rzFE1InZzucnmCJnmhqtbxnUig9QR2V7XB6giV6gtBmvs2kiNSRw+kJluiJprbXeyaF0hOKuAV2OD3BEj1BaPnfZlJE6sjh9ARP9AShj38bNkR6wuH0BE/0RFN7+D13h9ITikhPOJye4ImeIMxUaDMpIj3hcHqCJ3qiqVX/nkmh2ROaSE84nJ7gaZ9LmG/RYlKayEE4nIPgiTpqGpuw1/Myz1GbIvITG8kocGmnS5g20mZUkgoOTkPwxB41DbHYtyq0N4gWVOBwjoKnzS5l+EubWSkqOjgVwROD1DRTZN+s0AIcranA4TyFSHvhpiEi+8Chm2FtqMDhJIZIBBNliFKbP7RUdHCuQiSugjIaqQ0dR0UHZytEYiuaJu7sOz2UrjA5FTicrxCJr6BMqmoxK8Oo6OCMhUiMRdMApP0pHWi2i6EyFgxnLETaFDdNGNsHDt0UG+qmmOFshkhUE2XiW5s/pHJNDKcsRKIsKHPe2tChUhasw+SOSiyR9wOd/NCgEMe1tSFC5SKYBOcUGRSOn+eIMMKYov01ad9MRrThLBydeLR3bUPlOJgCFcIlhaDP6Rt5x7OMaLNF/Brh00ZD5VWYBjXC9kQj+jzMU+1PE2xC3nf+w2zgDDveiDw4xrU6ySn5Ap/zH3nnyoxoQ1G8vsA3sIMZKovHLKgRefIFfl+gqL6gZgzbyD8BBxq61+wMwGGy1RlUyRn41v2RdyLOiDbOxe8MfOuJpTLDPAc1gidn4HcGhu4MrE+LWOC4wEZnwMHxtlYm6P3QOzL0+25+5J8xA421a4aeg9CrtA40rgPOB6MgrwMWXQd8R4qWegbFBagRiUNq1Ij9hX/knXQzok0+8muE7zTMUg+3OMgqVkeKpeWhQTc0oy8PzKdFKnBEY/PyAPKHNrFFBOg5HXof58ht4CjBZuhBotAm6rh5HRA+GMnUsRboOuCjji31rJyDBKJLBGKzRnipHzKBqFEC0dcXlVnq+TwHCUSXCETC8kAnELmPhhZ54OjF5uUBJBBdIhCbnYGPQKyZWTWiDVzyOwNf5YSlpoMIkEB0iUAkOAM6gch9BKLggQM9G52BAAlEl1ikZmfgY5EEmUXSKIskvCwSNRNJgLyiS5QywRnQKWXho5SFDBxF2uwMQALRJQKx0RkIH/UjyFloBiUQfY3umKVmoQmQQHSJQPTrhqETiMJHQwsdOES12RmABKJLLFKzM/CxSDUTzka08Vx+Z2B8zoCagChAXtElSpngDATdGfgoZWECx782OwOMQHwwVi9B3wQ9nS4SPtJR5oFjSpuhtyD0iTtuXge8rB+ZOzYod+ztCmWpyafCgRqRCMRmjfBRP5KcgWgMqhG+DERHzUCUOagRiUAkLA+avjz4aGjJAkfuNi4PkoHQJ7qIAL0lQy99dJGUgeNHm6HnIPSJO25eB3zcsSRzx8ah64CPO3bUDEQpQI1IBGKjRkgf9SPJGYgWJRC9/TgcNQNRSlAjEoHo1w1LJxClj4aWKnCUbvPyoEDoE11EgJ5OF0kfXSRN4DjeZug1CH3ijpvXAR93LMncsUW5Y+njjh01A1GCBCJLBCLBGUi6M/AxT9IFDhJudgYggcgSgdjsDHw8cM1wxhFtWKffGTifM6Amn0qQQGSJLiI4AzpdJH10keKBY3YbnYECmUKWuONmZ+DjjhU5+dSi3LHyJZ86avKpAglEllikRo1QPjKwZmLliDZu0a8Rvn7gjpqBqEBekSVKmbA80DMQpY+LVCJwZHTz8gASiCzRRX7oHZ0uUj7SUenAsdPN0INMIUvccfM64GP9FDn51KHcsfIlnzpq8qkCCUSWWKRmjfCRgYrMIjmURVJeFomagahAXpElSpmwPNApZeXjIpUJHKHevDyABCJPBCIBejqBqLzMkwsc9d0MPUgg8kQgNq8DPh5YkwlEhxKIyksgUjMQFUgg8kQgEpwBnUBUPgJRs8BB2I3OQIMEIk8EYrMz8BGImpx86lACUXuST3lOTT7VIIHIE11EcAb0DETlo4u0DBzh3ewMQKaQJ+640RloH3esyRmIDs1A1NLnDKgZiBokEHlikZo1wkcGanIG4t7wXb9KKJ9KUFMQNUgs8sQpE5Qjz8kLhPaxkVoFzqNvXiBACpEnwoiCPb0NovbxjtoGTk1vxh4kC3mij5uXAh/xpw19KUD7IGrrWwqoWYgaJBFFYpKaVcJHCJqcrhJoMat2PpWg5qJpkFwUiVemrBD00nbtZSRRYllTM1M1SCOKRCNSsKfziNpHQBmUR9TUxncG5BFF4hGblwIfHWw4fSlAiUTjJRKpmYgGJBJFIhIp7oDOJGofk2hQJtFQmUQDMokiMYmNiBsfk2gE3R2gVKLxUonUNFQDUokiUYnNKkFfABiacGa8TCE14cyATKFITCFluBI9/dT4mEKDMoWGyhQakCkUiSmkYE9nCvG1nUoEGh0y7V7Y4U67Z0xg4+6NzxXbFgWg/LgBYYMjbHqHMHuI8NOn0SGmz6FuA1mDE83bjL6DrAYVsLgKuN6pAD+VCqiods4Mvdqoi6wGFXCwClQmpfdFBcSpVMBgKmDB8cVtKtBBVr0K2BxXAdE7FZCnUgGHqYADJ5e2qUAHWQ0qwHAVUL1TAXUiFeAcUgGbg6NKW1Sgi6wGFeC4CvQvHNSnUgEs5rcMnFLYpgIdZDWogMBVoH/hoDmVCmhMBTg4lrBNBTrIalABCauA6184aE+lAlg4aAU4jK5NBTrIalABhatA/8JBdyoVwMJBi44ga1OBDrIaVAAn/1z/wkGWn0gHBMN0QIGTp9p0oIOsBh3A6UHXQ3rwVPygAANCDQ4catOBDrIadADnB13/AkJ2KoJQYAShNeCwkTYd6CCrQQdggrA6zaY3OnAqhlBYTAcsOF6kTQc6yKrXAZfjOtC/kJCdiiIUYEzowNECbTrQQVaDDjBcB3oYE56KI5QYR+hycJhAiw50kdWgAxzXgR7GhKciCSUWEzoGNhJv04EOshp0QOA60MOY8FQsocRYQsfB/tFtOtBBVoMOwCxhtUF5b3TgVDShxGJCJ8C2wW060EFWgw4oXAd6GBOeiidUOaYDEmwU3KYDHWQ16IDGdaB/MSE/FU+oMJ7QKbBJaJsOdJDVoAMG14H+xYT8VDyhwvIInQbbgrbpQAdZDTpgcR3oYR7hqXhChfGEzoAtAdt0oIOsBh3AeULev5iQn4onVGBMaMFOcG060EFWrQ5svojqQP9iQn4qnlCDMaEDG4C16UAHWQ06gPOEvIcx4al4Qg3xhDWm6en41awDnWQ16ADOE/IexoSn4gm1wHSAga1+2nSgg6wGHcB5Qt7DmPBUPKHWmA5wsLdPmw50kNWgAzhPKHoYE56KJ9QG0wEBNvVo04EOshp0AOcJRQ9jwlPxhCbHdADt5NCmAx1kNegAzhOK/sWE4lQ8oQFjQrS3Q5sOdJDVoAM4Tyj6FxOKU/GEBowJATMnW/GW5Vtejaflc0zLe1+UKF7Pp4WnXLx06UjrEx1QDb2+/fLrk1VxVd7qy+lNcb2YlOCNzqbjl0UJ0NmzO2TObwF5UsHlRfbsYj6dL56sf/fi6dNnjzb/LD9u+U0p+m2xWG4enVsmjePGSie00+VDT2aXRfk67Pqdbu9m09xiebGYXN+p0pfjVTG7eP84M89nX9ybxbL8d/589u2byatVtpi8frPKXr7Plut/Tmavs2nxavVp9mz9rE/KF3n+rjSRF9nTp3cfbV7Z3YdP9r72Scaz77KPBM/O97//cfYo498JXj7b5GKDV/ni91R885I9hr19BZsONhvwJsWyiuQ9ixgSLxoT5iN83SNKW683jPubXhU/rK6nJY7ntwbyej69bG+HadTGLt6WN3V3Gc5qLiHgS7CWS4iaK0j4CrztIfKaS2wDwZ9eMbmvtLl1H35wX02mq9IS65W1yR/nt81bbu76Sdwr6wiQMZm9mlfEnK+TjO4EyY2rJro+35kMccBHh4Arb3zXutNi+6BHx51twQtw1f4+++w4a61pXVpVwxs3oHZX7edo2p131G5WayEcksErMvi9DAHJEBUZomJgiAxZkSHvZShIhqrIUPcyNCRDV2RsnYWBZJiKDPMw0iDLsBUZdqsfmIK4ihC3FYJpyOdVLauoKqYjv6xKqbhzTEu+qErZqivD9ORXVSlbhWWYpvy6KmWrsgzTld9UpWyVltnG5anWO3o6mNvdBYs4hMai7lMcyX3+tvradEf/+buqENPRgf6+KsR29KB/qApxHV3oH6uuPO/oQ7+sCmEdneifqkJ4Ry/6VVWI6OhGv64KkV396J+rUlRXR/qXqhTd1ZF+U5ViujrSb6tSbFdH+teqFNfVkf6tGj7kXR3p36tSWNWRIlLevSn3ztUQYIt2uXt6gQasdT7VoT5VHsmn7myWREeHuPsKz1nFFb1AOjYSe93mHXZV21fKYlCYD9iJGLuqo/TEVO2ZLNSpZB3oIX6w9y94HADOjwGAayRQ23e7jDoliIeYhnbDNQ2GJX1RG7GLEFOJjUd/CSDCauDtpW6JkMiQhBhtBtNQo3bqsm/eUWMf7LrTMapTw1MXKpx1XxA7Qlp7HWISQsQzNZWTJ5MFLUNmwF3LfTMnsRwEz0wCTp4nEpI8NCCfSVyZdpM3sOkBnDoTxAYFH2bg5UC+El0DokaNT1znaU5EyA40zIMdfoTHq/F0WUAotthWnb90NIx4BwZCRrasD2Cb1ZAp5FnhwJGZ3BOTCs9EL0FknXiHgprtjCWtBry1hnLoFRUPcOpdpbKFCMaRRpx9dmQ/SdjX+fbaihg38qDikzg2E6MxgdwpP/n8q1+dYjPQbjiSGGBwGbSdVn3pKrtbI3wsUKAqcUGNKFTn6e798mb//ue/+hj3cSju2431FfFkhIfxHoP3d1CgoKmBQhh5MShQSBG7LzoQRH6Ch/ETg1qISMSSFxgifctdSJ1YT7c6RznfxaZQcWLxpgijG5IH4+BcZklM7xcdMiH08AwlQoSmiK5LdGh5UTEV0ctRmt8dw3UJ4eHJFMKkakXES4S0qRk0XuSx9AKcTq2J5/JCBjGiQ8GuHhOPtXFPMzApQEyp9hiWa5Hssdl/eio2hEP8qyT2gBI6iIEdMp6K7F/Bk2BJ7OEmTBCbNGz/6rE27mm4KTWIKbEfl7BBZNSQ7dFR7VGC+TSS2EdLuCC+KvnS5rXPYnmHnoMwIq0iw2iVYftXi2Vd7PlXMMtDErvjSBYU77Dh2qgk7yfRvYfwNNPQxPMCyYP2JkPG1pMHLCFuR3iakWliIoIUQfEtG7T/9eSJ+xBXoP8VJhLmMij+HbINk/ej6N5FeLgmRewtKFVQfJzW3mZr9lm7hfy3L9uFOG9E6qD4edj+24QhrjkYP3vicUWcLyKD2ocO2sYt2X+Da7P2YGuI5znSBp1mp7W5mb/w1BJJA52teoYDGOJZuezAZ9nkvxs4RjKi9TbM42Cq8pDzdOX6gek5Z9JIK7S0J0lEratBaUWPWA+hgmqI+oLOPTinyRJWHtPj0DhHRTxIVUGzdHpvWP/59TfHwI6rkFKwPdJBUkMqsoEKsKjMohAPp6hMgWlHhph0qYIauPTeEo9jiEpgVbEeQyWeuCkVwvj2Bbrd4RPHaoitoO46yjM2RhMr05QOGQbQ95jlkyNB59sgcixBnewrg2qfegPeCbb0ikzXoEcp0mOYhljXpoLKpwaNrYd81QxKxfQchxpi8ahyIXT6YPAkpiSMPIij6SbdMNV5CF0+ZButscERjTrzYks8ztRBxV1p7aS3ndsLTaGmTZJ4XKl5CN09cP/qSafWaMot8bhRB5WHKdNLzB6dpsSIQwV7eysesYBIy85tmZTpE4P2ND6DtlrcQAQa1OtTEzNktQo6gzB9oc8ObVOEEi9OLrn0QEcsHtG6Ozt9Utt6QHYeuklkm5XVb+A9Z68KqlTXvu09MdtZmyCae9BLn4TYa+3JfzTEwyNtg9jtIXtWSfasEotqqHs917n9Wopa/GdBzQCZPI63NDkIIE9LY4cjp72lEbNG4q7PsKBTi0EvfcpA5udLOyOWdRgexF0PeemrybYnHjR5oCV2GTAiiKIedpyJGZtvZ0A8kTcyiMgcdJxJNjaJGRtxB29UEJ/Zl5aX/BQDwTQUaxhNRdoQiTMT1EqnN9idBDrMTypsT9ACLS6pHnoTlAM14NkP2lNrqHWYUbeHq7t/tzngBXDR9boT1PGnN24jP8X0OgPxeMZg8VWL38Al1WPvgmLrvjTuPcmsSYMt9+TAzhDTBeyWUVpejaflE0zLu16U+F3Pp4XH4+ebsd3UJzXd9XJ97+W3J6viqrzRl9Ob4noxKUEbnU3HL4sSmLNnd4ic3wLxpILHi+zZxXw6XzxZ/+7F06fPHm3+WX7c8ptS9Ntisdw8OLdMGseNlU5op3+8n/vt1i90ezcb+mx5sZhc36nQl+NVMbt4/zgTz2df3JvD8nHG+PPZt9fTySor3hazbDy7zOaXl9nLyWo5ysbl/1rfQ3Y9nixG2epN+Y3lBpZRtnwzebXafP+qWLwu1n/MVvPrzS+z+avb35UCNpB9mn17XVxMxtPsTfmL6WT2Ons1X2Trx1z/oHzEycUGtLpp6pt37bHr7ZvY5C1tIJwUyyqe9/PeUBchK1lGJj9UaNE4BnNd5VXfNf7+QVbFD6vraQnx+a3lvJ5PL+ueo9LI1+7OuS+X47flbd9dVdS1Y4OvZ8jX03XlsvD1NPl6rO6C273iT2B49KLyPvWntMXj1WS6Kq2Zounv5vPLW275ZlMFUVHxkffHF/Pyj9sfq/sfc8KPl6v5rKj8mt3/WmwWBaqfJR7joa/dHPO1q5DXLg7+2uvnVBAz2g3uCisqL3sSKUvBtFJmnWdziurY3X2JZ9piTk2zxQW1hGuM2JLCQqd6stpeRqZyTI/3awoyISCJfQkcCKRJQDbOmCFnxjN2CChZHhKx9sVNn9/7aX0SP30gcyRm6bIOuw6bltqHL9t5VkRyQ1W980tccJtKELPXGMdVwiWzPpZzphq2ABfaSgDN00Lb5nl3SWCmQ1bXPWnE3SmT3UPikwLMDp+piALsOdKBMgAYMQOAKdzNGhTCn/vKyzxZowyqnGHEBACmgwJfnlbIunVvDzsRsi7uSSMmMLIw7ikfTGcaoutrQYx8UseIJ3XMBtll3svEnOMcsmITt5kvInLNWBJ+Wg+uw45hq9AqhRzDhipmpGPY/zveKSzjnY9hVcRj2EWxvJn+7E5hpTzlKezX30Q6hJX0Q1iexziFrbw376moaT2GpR3PSZFORVsz9IjdidDXrtKpqOdUNEfPo8muSSSqdiebfzeBr51hdZ3JeZ+cCGeiBiOAJE9HaXTf18TQQ0DygxxuS5WApBJCLbR7fggoXUj4mM5ODmqNhzvWljqts1iSEPl0DE1jYgc5Eu2wKzTJrI/lmw18sA0HTPxn3tsj8pGoPciJGXikXd39pCPt1pVzj4VVIcFR57MXibtZlY5En7UfVvvTC5BTtWiH2VKmE1Hvxv+QiSacSDt1OO2WOlklmKigQiKe/UO0gx12y/7loBimLDfW8n6mMciQHUnEo+5qOJTSFMjRKc+pp8E13/SdZHcJc3qCXX6CJhJYlkJ85HgeFOYMOsFEheUGtS9we7ENA3I2cNH1ysHABJWKamAJKqGKHSlB5f+LmKAiqAkqfCdBRXfKT9lJTJnO39X3B+h56ok6aerJf0bLPVFiNxWkmm2iY2SbKNV2iTxGmb+SLZeoTWFBcylUSmHBTh3iFParlMISKYUF328qkc5RvFpOrdSPm6xAhpCn09H2Q80D1QCzQ+UsqNRt41hnm+xgSQsq1eJ7C7k7F2rH8LQdsg5UOg47ZGmn75xTNFs94aexqvFVqjVEK7ihwU77jD+1tJ+Q2UCjjlR1ZgJU2xR475Goo+8iUkeyK3Ukns++Kl6Xf82erZ/pyeY1nL8rreXFHVl0m7VRZOPX40mpytn/KhZzhBKqSVPpxAeR0l1YpWFsHpDu0p630jpQJgYXVHkM6SsLkjGYIWbJF+Q8Qh0S27pnmUico9UhVWFOJA5xcxmnDKmq8XK4p5eyNaqwh2LQqoovezmA4PxIE7FivH/beVGWKQcVykGFRoU0NxxwXtaLFnJXkBRQyE3uJnCgZgKba734LGLEbQ8VcV99WBE3Z4eOuJ8eI+KuPIYvAHYxAm7Ojxtw8zwF3CcIuKswp4D7qAF3VeNTwH3sgLuq+CngPnLAXV3MUtHehxxwV5D8EAPuiEOUWOcpSub57PPpNLu94rIMscerbB1eXy+KZfkisvksK0rXUyyydRA+yoofLorr1ab71urNfFnc/uJyPvsfq2x5c5Wt5v2OyCt58h9yRF55DF+EbKK04tJ0zt3FaMUlU0QeYUAR3IpLp4i8PWJxaESOeiXZq4Y9//7nv36282gONmqq6rzkcAf67nZSO1DTnvwwLbRMssgIaXCuH+moUg9vwx2SF+7tqRTDIisZqfAiyZNJYglsQWmMhPxTGoI6US8dqRd7EPx4dwvM+zQh5kn/+kpyT985X8er5rRLEStHtAKnwPrfc3KOKD8kg/YkHoN2W+DZhUFzP/27WGaxT9s3VcgHeB/95ObEz4Obq8zROk5+qggjA0OmlXciA+Fp5YkMPEVRs0hkYPSiZtQPJu7hWMXN4lDFzSKxgUesaOaHHjKeLPJ4pc3iGGPGh0wIHqCcmTzBOAahJBIlCGzT6XbJw+aIU9t1884DilOpBFbFfrBh4/JAw8YTU3wcpp/hXYcjNWYXMJn8s4yLwQHUviHGutmwCT/1tW6HbTedEgQNQJZknl3Cg8mJM3I7nxEE3nu0sraYhwTsuIcET9Mhwf6hVf7zOCRwxy2pq7y2o5wRSHbkMwKXzggiJAyjZwRVmNMZQUDCMJ5lWtX4xCsf+niAHSbLNE+88tHzvsXBskxZIpWh4wDt6bLnpZX5gTJNeTLLoyd/iwMdEbjEJHZtekk/P+AHIY1599U0nQYRQhia3fKwCcqHmt2ayvg7HwblUXsaH+6IoGrQQz4iYD+3I4Kq8aYjgg/8iKBipR/mEcHTmEcEPDWbvm3OcvBk/tuo6vDN747caoMD5QM6BlXPj5zOz1M6/ymoep7S+T1U/eH6vcnUbc/b7c0dKgGf69Rt745ujfD+XecwIHEyKAGHFX3nLem9fmKc2HJPdWy556ihvjtkpP9/xYz0yROJ1W7PvTL0/9tsfcGClrjzvphO5+9efEK6+VFWKuE8u17ML28uJrPXm/nFN9elu8nejKev1hOM158siuXNdPV89sv35fevxrPJuOejjPl2zqcIdOO+1fCTSFOLK31eBfdE1irK3kGQL3irvsF7B0l/Qtm6d8A3K52eEI6aKz1G8xhRc9PKktdGsPXBc5MMViuDQzJ4QySNyBC1MiQkQ9bKUJAMVStDQzJ0rQwDyTC1Miwkw9brB6Ygrl4IpiGf1wvBVOSX9UIwHfmiXgimJL+qF4Jpya/rhWBq8pt6IRYiD7ybVrg3/2H93m8j+L3fRfB7v4/g9/4Qwe/9MYLf+zKC3/tTBL/3VQS/d7tJ2Mo53wpyBHJoh5aSuaswUzl0J1/H8MB/juGB/xLDA38TwwN/G8MD/zWGB/5bDA/89yYPjAhZe+WtGK2U0DuN2smiLuereteWQ+Nbdo9xJUq1wcT+8WLlvCexMo8QK4sIsbKMECurCLGyjhArG8+acTBXXw22bYxg20UJtvMo0XaccJtHibdFlIBbRom4FSXkbhho0i0lyqEOVp0iKNcxonITIyy3MeJyFyEw53mEyJzHCM05jxCbc3Gs4JwW6FTEBMToXMYI0rmKEaVzHSNM5yZGnM5tjECduxiRushjhOriULE6lj4Qrz0V27Iv3PYjYYAzaaQVWpqHZyWff/WrU+TARmtgY+GyEzKIoncgnt+jaE+D4l6Bl3dnSu4k59/jtmiBgytSyFqgkhb4S70ae52DBYEObkdFxlEnl+wr+vLugsjlY/79VJsa8PxgJSnM9k4N1hu0KvxPnx4DfeOtCtutHem+gHsltbh27tEtadv/rqg1xipkDPCwdWnfze8gTu4EYHd/iUtu9ywqUJuojVB1SJprX7RpvZ9Sp1mb6IEkFChyGN+dv1OLJTv0g8kT/l1iDzC2ED6EpefvmqgBYCuZ6m5T/8yb494WdwWMZmpUBheya2ysqMRbyTCJovnz3zV6WtXyvOt2Y6/M2YYwSL772v27IDY+4WATmyrxkByCz8yJBASP4hB4BzLR9M4hsJO4AQ61mhG+1di1/10T4zUOtqqp0ggnNU6phWR7pVH/ffrSKM4wgnfP7YLUoaAi3YE6dL2zXf7Qdr/roeUS42SOc3iVmo4B+VIin+GxEhPoT4lsGgcbylSptORPG7CWGMu+51Eh3lUQD1a5DqkEHIw/Ra23DhHi4Rjv0OBApei0gR9sQ0TmqLfc+TvVxkAuqUolJ29ai7PBzqj2fCk4QE0Szw04TjVxk6JT3HKJcYzAc7+4S9FpI9fusRKB7ua7+VOB9iDOkz/1Yp1jJ7V7NCq0u5TEEiiBJ3wJlqJTn/XWIULkX4QIOkwZ8KQMBk0G1MTdgpBBXLbs5Qp3nLQXzqjnkgLb6KmucpsOLIQKSpTrCchiB+XPPjuSI/QQLxwaASk8xLfwbD0M+Zw0+ErURVYHUeqyL+fjD7Xr0VFcCHQ+eQDHYILY9yF7f0GeVMUlBLIlg2yJINug1NbheP86NDxEEVcQtr5NkGd0hyFXUQVfiZiCL1wQ/T9o369P6xZkHnROMOjI31DBkNgmmnWV2wgyC0pEH3jk7zvg4VCHX+nJJJSevEZDLqMIvhLxuELyoOOKQXt/iM05gGMQQScbQ/b+klycIqBJXZI8T0cSZwFJGVSGMujI33cYJaCpXlJ4PLKCuZgR7RANvhJxfolUQUcrQ/b9gp/YLeigNgg8FbRs3jY9HIMGXEtDRNEENUHgg3buGq0DbsQWl9SGvYeSl55iJUXMgJA26NSPDzn6M2hhQ9dxnQdyGy7otCY5/1tDI5/C1XyzBUWV01BUHci7PDn/W0txcJOHJuePS2qzYA8nrzwVtJrI2igWdOg3ZOfvywsOcQu+ao4oboMHHdck50+qXVTkBmlKQIuDIKIsQkZcDntxUBztD9KILS6pDXsPZa88OqmJyTxKBp0KDnlxCDF7X7J0FLfQocWZTW6BtvCT2+MpqAxTea6riWyt0kHHPYM2a3IvKqWimjUxh0+ZIDY3H27NmIK4OUXOwFHEDByF9gjTKGyDaQmkPKycxEzPxMrB9klSkfLwlAsidPMhZ2KQcytaEnmD/IDOgyjZAXtwDRFsmoy0JmbRaLCStMrBJg/+8JV7CDEF5dLoPFYmtU+SjpRLp3kQKztoD24O5cHJfkAE8apD9uAQC6bJh6uamAujJejBZfLgZB5qx1NCZLcWsTLifJK0ilMHqVUQdZpicFJ1Sw56cKof0EGp7EP24FCaiiav1ZqY0KIN6MFt8uBN4Ghs/IEnBtex6ll8krSNk9OsbRBLnmLwg3hwqh8IatPP7HA7ywiBIWKIvWVMHpKhPGRElMehAZ0gwIzhdpdufEE5VTNYSPrikDVDe5IAfXgbTk5uBNMNCVdq0yxP/oolHoSYIBqN9XSO23GSHOikqIF4d0M8yTZBLBob9jxHMh1iIMbN+Ih0TcRWhuQkssFPRJNgft8eTp6UM0POchHq6HfSpp8M2/o16mcQeTfwdeNQvsd3tEY8XzcaZIgMCuyHyxChndPppI2BeEFDTGI1JiSJddgxgjbYWr6XRMUwe2QAtwveiYTvBNp7NOheED045F3rwbyGJxaxxOQL44KYKj1gZMnDWTXU8ch69h22yUhtUGUs04PeREI9bQxxXKZlQUv2kI0LImetaLS99Z/qsdnSZcur8bS8x2l5X4sSn+v5tPC4PfapAp6Fqi0CvKOqrkB3ZMlJB7Y2Daz89mRVXJU3+nJ6U1wvJqV6jc6m45dFqQxnz+604PwW/CcVHXiRPbuYT+eLJ++L6XT+7sUnzx5t/l1+3vajj6bz2etRdjNbf1pcflxe7G2xWG5eBbdMGseNlU5otzaZyeyy+GGd8bZ+x9sb3GxWlheLyfWdIn85XhWzi/ePM/N89sW9TS4fZ1o/n/3t7lpZ9KcZZeXGY55dL+aXNxeT2ets9abIbq5LC8vejKevsvmrzSeLYnkzXb/WycUGzRKXPXPbgOBxMdsXsgk9NthOimUV6Ptx37C3clsiQIhDeasHn1U90Sdn9aOk7h9jVfywup6WMJ/fGtTr+fSy7im2dJu4taPKc5TL0dvypu+uyVRdK2D4gop8QS7qOpnAF9T0J5R1RRbwBW3YE255i5/Q9yhiJafU7V6vQRVfTaar0ovUm1bTSpbfMgo3d0V596Y1AmSwWhkcksFrZQhIhqiVISEZslaGgmSoWhkakqFrZRhIhqmVYSEZtl4/MAVx9UIwDfm8XgimIr+sF4LpyBf1QjAl+VW9EExLfl0vBFOT39QLsZsQlRoTNm3HUb8nj+T3fhvB7/0ugt/7fQS/94cIfu+PEfzelxH83p8i+L2vIvi9293DVs75VpCrFfQwdn03n19Wfi1zp7ZKlkN38nUMD/znGB74LzE88DcxPPC3MTzwX2N44L/F8MB/b/LAiJC1V96KWZ9v660oB4m6nK/qXVuOrAl6t2kCcVSrRdcMfYJYOe9JrMwjxMoiQqwsI8TKKkKsrCPEysazZhzM1VeDbRsj2HZRgu08SrQdJ9zmUeJtESXgllEibkUJuWvJTLfrYAXNwTrUwZpTBOU6RlRuYoTlNkZc7iIE5jyPEJnzGKE55xFicy6OFZzTAp2KmIAYncsYQTpXMaJ0rmOE6dzEiNO5jRGocxcjUhd5jFBdHCpWh1YB2+DlGX587irDIk1P6mD5SboDk/PnGZQ/zzRthWYdjq5E77Bjp+ns7OvHTK6b6SCpDXti6SrD616qrGlPsM9PkWSxi8+hrJg4m4PhVTBVLmPYHpiciW49YzuYpwaWESsdGV73Ut04DdsnC6xHfoul4pJa0efEakSGV5VUcgaG7JXploxaLifmBDMdFAmrnlhuvt4vn2JIAtSvj1MXRxMU4vYEFJ6v+9GeAhQWMq6+ERQbFHsOHhRsHCR1M+iCwshBuS9SzODrisKJbeJ4HhQRDspaSAu+FxiiG+MsKFhLwLTMrCJ1gmoEBuc2bMWVieH25uOefQ9XIcMJG/HCGQxrEl6Xt5pO2/VwcNcjiXwFx/kKa4eHHYkT2q1Z9FmjEBimZHvswELkyR5r7XEHUU+dOofq0AWx2zjvwEywhGf9ejeiB42tsQwnYmeCWKVB+1fuqQn3WaPQIKbEniQ8jP8YsD36xupxz0Q17iD/SuzzwV1ICeig/Su5A4zIQVsk9hAUeRDtNWz/6unvwz3jzoUDMSX2DhQsKH5lw7VH4YlfBdSPjXu67ShiqYbgQfHrkPEk56age0nuG3BLPDUVIii+ZYP2v9JjrR5rlhzE3ESyZxkU/yZ7bkbcE/8KqFsa9/QGlzlxPVZB8fGQ8SZntaB7Ve7hHiWRWxI6KH4etv82YdYswSw04eFDJJGTEibo4HPA9sw8K6jwregQPyw90zcUMTVEdOCrXMK7fr1t8t/gXtjX0VYpIrYwd6XyPPnvBk7KZ607/taCmKs49izzkPh73eVhqPYsPfG3FGH88g6exAwxGdSCcNB45uTpRjyUfx61Dr9txJaHxNeDwZbIaY081ozyzx3tVYTEz8le6X3+9/6uIf9MnAUjZUh8PGg8Bdn/ontd4qwXqULi34H7V41aowczYstvqXHMeLK3mppi7o1fd/4O8ceKWKQlDY6nSHjWr2dN/hPcaypiEYS0OHYy+c8GzodsbfWYUe3NheTbM9NLzB4dibMXSPGd8jDuiphlr/KQLPu+IHaaQfOcOrWDS6iukhisKBaSvDJsYxNQpavyjH/UxPIHxUNSUgZtbII8IkdgfpR4Gq1EEBM6aGOTUK2/8s0XJuYCKRnEbw7Z2CR5lJ7E/CixjEGpINpr2CsbNKlNeYhnTTzsVTqI7Br0ymbIKxs0t1IR6xRUGEcy7JXNQIh4ODJN3GWrMGZk0CubJq9smB8lHuioMIKkL71wdqD77LOjYAe5P01MIdZ50C66L4icAhCFxfWevGBN3IlpFpRj1Jt2UqfoY6mhjr/awzFq306NyEFqHrS3Hnp/QyUww9o9DNBQapkhcl06qHlwX0DlJ1npQDP17OEMkTDRMih5qC+InaRBsIbaV5GXujAepDd94Jxhip3GNypsCdvzjVBal/YUYRhi6aoOY1NUP1t1H8l3YpYosC15o6WaoMQhNeTm6hoqPdJEWkvbIFpLDbfhufJ4MW3CopMGvFxIP20mhouXhrbhhlgeYPKgTZkY9BoEnYoZYnK/YUE7qiFbiDoIHjykffag8YBSNAzxDNKIoBWEDRgPF2Ife7sc3XioQvlpPbYyaDViQ+YmTI7tSrH4ofkEzRCzPYwK8qMDtluDxRmmGSrThM2WiVhejaflPU7L+1qU+FzPp0W7R831ZtYy9Vni65VB7910vXdFvvfa3Wv57c1M9sdnL6c3xfViUirU6Gw6flmUanP27E5fzm/V5ElFW15kzy7m0/niyftiOp2/e/HJs0ebf5eft/3oo+l89nqU3czWnxaXH5cXe1sslptXwS2TxnFjSyi10z9uB1Bvht5ub7B8FZfF8mIxub5T+S/Hq2J28f5xpp7Pvri33uXjTIvns283V8qiP8soG0+X8+x6Mb+8uZjMXmerN0V2c11aYvZmPH2VzV9tPlkUy5vp6vnsl+/L71+NZ5Nx+cyTiw2udRO+N3B43NKPlQHfJYIblCfFsgr5/Qgc2MPJrR0JGebhfK7qk7P63rP397wqflhdT0t0z2/t6PV8eum5Zb47Zr30I2/LO7y7Jhd1DUPgC3LyBW8nNu9Wq8AXlPQLyrrsD/iCmv5KWR2pcn/Bn9D3aN02s0Hkn9I4sFeT6ap0HvV21LTU5dXR8hU7QoZQs1oZ2LBxXisDGzUuamVgg8ZlrQxszLiqlYENGde1MrAR46ZWBjZg3NbrB6Ygrl4IpiGf1wvBVOSX9UIwHfmiXgimJL+qF4Jpya/rhWBq8pt6IbZxenztxOSG0A/1e/xIfu+3Efze7yL4vd9H8Ht/iOD3/hjB730Zwe/9KYLf+yqC37vdNGzlnG8FuVpBDwPVd/P5ZeXXMndqq2Q5dCdfx/DAf47hgf8SwwN/E8MDfxvDA/81hgf+WwwP/PcmD4wIWXvlrRit1Lp3x0+iHCTqcr6qd205sibo3YnaxIQ1i64Z6hRrho6xaJgYq4aNsWy4COvGehhP8MLBY6wc62zB4KVjnUV6nLWDZocVMQFLyLoEPnwN4SrGIsJ1jFWEmxjLCLcx1hHuYiwkIo+xkohDLSUvkMos1+DlHerl5QkYkbwnjAiPwIiICIyIjMCIqAiMiI7AiBiPdz9YQF+lVGwMSsVFoVTyKJxKHFKFR2FVRBRaRUbhVRSFWKl1oHY3jCbmLjM8b0xUWvjbnuSN6ZOc1O++c/IQZgZVjDBfe8Ucb79Yqwsdzr140oXbd0puYOp2tQYcuMVcoDYQ64sYni9XOf/qizasw1J1kloWRm4pznJoGBM8zMs/bKAWfzw/T+UJ/7YVuAl/sP04h8cB+dtJ1moAnsUntjk5XPey1v5Y6EOVaL4B1MpTE0wd+MHw3D3heodoHwZOe/CkWtg24+OyuJhcFgt66E0D405sHCS2EEgtNm3i5lfX48XmZh+f/fuf/90ZibWo6/ffb/ZB379azK++n8xKMWePX42nywLByVMhyjy+keWNOZr1vpi6muKj0irZPQPypcSYFxtqCPtTYtUVsyGZgoPxpyimdW3XiMeCzGEetbqBTR61ASnPeErmGW/GoIoFQWSuOM5cVc6Ahx2dcoh/8o2PVp5hEdTm5rwD/2RSdIrjSVzdOAd9qU6+1IOTh5vjnriEcSw6FUTml+Ncj3QpOm3kY7CRgP7dfEd/ivM3iqXo1IdpnUcl8i9cYR61Sqgmj0obxLLnU32MAFTdLojMDtdB3KnspUc90lGaJA9qgVoRcdtVblPJKjdBdKoccGdnBvX4OAB0NijvoSfQicP3y6l/y54IhWkIXU9HTG7QjqmN2hF6JWJvE+6C2N4he39BPzY1IbRSy9wGYrtPkQeRv4P2/vbE0IVlOg3H+9d5a8/ZCoO6E3FPm3nha2pOzrsKvhKRlxY8iJcesu/n5EFWQkLbc9lVbqMDEUFU9ZB9P8dOg+JDJ4PyGgce+fvOgjjU40p4JnUKAY+sGFEniIJXIp6ZCBXEpA868jfkpTyIsmtxIcSxUEIHEeuD9v7yxNCZoKzmQUf+vnMrDnF6wjPrQeCzLke08zb4SsTzNtGBU6xE/rwvboFJI63Q60KBE+SmCPqajmWQEee0C5y7E7p3KJ7IQ1i0NqkRW1xSG/aeUZ7Ss/dXxOxDmQed+vEhR38OTswmu4WgdESi25As6CwwOf9bQyTTeRIagyeJTYglDzq4GbIBM88Omw7tvoGOjgF9B0ovT+v+7TtmcM1xk1njktqw92mSR2cVMX9SyqCjwOT8G5b4Ues08BYtgqr1JHHmlVRBJztDXhzo0DEBK0EMaHFGr9JqauDOX6Ll6I1mi0tqw94zvUZ6aCFFTPWUJojyH7RbsNHcApQKKolZgrJDfadNbqGhy4S3lqXJLUATLKUvh4/K5bggNjcfbjWagrg5RSZ2ar5Zi5zKwa4KGoXtQFUW+U6FxWfx6ytWixukYE16uDQBJXtJFyuR1ydJsTjJXIoFEbr5kHM8yZk7LYm8YX6AB1GyQ/bgUHqdIiOtiDlaSgTRsEM2O3oOJWx2VPAkWDaep+W3ybJ8vfygRCjFY+VS+ySpSNl0SgXxqkP24NCeSZHzrBQxz0rpIK40BU6kYkcBenAqeAb04DJ58CbL8vXihCollYqVE+eTpHScSkhlgwolBuzBNcSiaHLYp6m7JxdEa6cY/BAenAqeBimwKmudPPhDT2ixftoeD25jVbT4JCkXJ6tZs5B8WBalD/gD/bizcVgdqm7gF6fgwfe6DdjuzPfIW/fcslYQN/I6KBmO9XQexHFOv+h7aQ1ls2liQoMOymYbtNV60ga0h5OhdysIvhJUS6U9Eb8hnovqoFw3NugpMfT9mYZSXbTvuMtzJm6Ix2FahaRJscHPBBEGSznaw9GTIKXJaXbcHv1O2vQXrPNuXPWCWMeBRyyH8k2+UwdiLpZGSUmDAvvhbmnRPsT0XaaGaizJOwsbwi0NOTo9GHIevtcQp8ZpF5IxOfDo0JMxqXPMkxL2C026c+g7MWE7l3rdM3nQnlcPWvdAItoQO+0ZFrRb1AP29BJExGOTRjRBxINc9pAhgqh/Ixv97fpP9dhsabzl1Xha3uO0vK9Fic/1fFp4jId9qpDWXmSTlug9Wco91b0xcolAzTfLey+/vZnP/vjs5fSmuF5MSgUbnU3HL4tSHc6e3enB+S38Typa8CJ7djGfzhdP3hfT6fzdi0+ePdr8u/y87UcfTeez16Ns/Vlx+XF5qbfFYrl5EdwyaRw3Vjqh3dpk7uZ8883M8e3tbbYhy4vF5PpOkb8cr4rZxfvHmXk+++LeJpePM82fz759M3m1yhaT129W2cv32XL9z8nsdTYtXq0+zZ6tH/5J+V7P35X2+SJ7+vTuo80rvPvwyd7XPsl49l32keDZ+f73P84eZfw7wT99Pvvrm8kyK/8zzqbz15OLu9vY3MMom3xafJqt3hSbl5G9nKyyy3mxnP2PVfb8bFl6gX88Pyvfz+RiowHPaualb4DzOKbta9yEwRt9mBTLqnLczwVDfZyqdOwyJszH7a3x+d4SX99G+v6mV8UPq+tpqQrntyb3ej699Nyz2lja2/Km7i7DZF23G/gSecslOKsrpIEvwdsukdflKtxf4qd33I5txSMZsbmCH91Xk+mqNOd6bW1aUvLbTfvNXYXdvbaOABmT2at5Rcz5OkC8EyQ3Cw51tWqPDxiV/8ctKW981zowWmBxooVjdc807bkBTQsuqN1V+zmaducdtZvVWgiHZPCKDH4vQ0AyREWGqBgYIkNWZMh7GQqSoSoy1L0MDcnQFRlbZ2EgGaYiw9zLsJAMW5Fht/qBKYirCHFbIZiGfF7VsoqqYjryy6qUijvHtOSLqpStujJMT35VlbJVWIZpyq+rUrYqyzBd+U1VylZpmW1cnupZp3bSyHr6eDUtWBZ1n+JI7vO31demO/rP31WFmI4O9PdVIbajB/1DVYjr6EL/WHXleUcf+mVVCOvoRP9UFcI7etGvqkJERzf6dVWI7OpH/1yVoro60r9UpeiujvSbqhTT1ZF+W5ViuzrSv1aluK6O9G/V8CHv6kj/XpXCqo4UkfLuTbl5roYAW7TL3dMLNGCt86kO9anySD51Z7MkOjrE3Vd4ziquCNhzUdcolnfYVW1fKRtwul7rlooRjy1ZB36IH+z9r4cVxADg/BgAuGZSth0aYg0o4yGmod1wTaOmZW4bHsQZtkyEmEpsPPpLABFWA9+RHrNESOCUXFVJp9GmJwffp2lbq7BRlp4Zs9T1RuGI2d4hxnkf5gN7EKEuMzpomTEDXmYk3OitDS+GDRlpxNPgeIoh+kTiyjNqrXD12CCxkyazQaHFcLwiqZ9P2KB7Tg0HHZSWrZRCATtQWjbbSct+cuS07PqyjDxkon3jOOoO7IIc3trWzaqgNGvuWSs5sSib43xFpR5CqwFHKzqkY2UjHjxoB6Z6snLl6+a5p+j8D1WySmIIyEXQJqsnoLB8/RynAAUb50eMF7gE4wWGInKkMq5///Nfpy/k4hDF5y36JKaAcRW0Vx68t8N6fhFn0HAdtHkavLezGDcriEwfD+MhBm8rYJNaQY0NOlANqu8B9FHO+xjU8p0TK4K5C9qiDt1MWuIA4njVhmG4OHNQafihxXDbNwoPjy2gtk+KilcHXkAlvC5vNZ04mrh5BCGp624jdh04BD087Op5U401yNtr4shATKn2GEZBJHskNzPY+7s+yHD4sEyLIeNJbogoFGaLktgTV4SxFsP2r552YD5rlBLElFiLLsJIjwHbI/e0XNu31/YWLp6hfJyIZxhbMmT/Sm79Jyxoi8QB6sIGbeGH7V89zbqF5xS6ZUQmadJuI6YuKH5lw7VHmcccZC9EnHmGMg+KXweMpyA33kP3kkJijfwbsWVB8S0bsv/1WavwtOJWAsRcRbJnHhT/Jnsmj9YLm0UvNDqvtgFvERQfD3k95mT/De5VvU29iXsfKYPi52H7b99u1VPlozSIuUUHYDZg3oGT0smea+151FqJxT2D99ARx/5297V4d+CrTMK7fr1t8t/gXrjDUMV6bDtwVzb57wZrHAVxVt7xlVR7tSH7ZeX6MgSRSSOt0OvHOUF2inQYepqYhypdyI63L+jcg3Oa1CHpK/WDZssp6nTRPKQha+8N6z+//uYohzgypJjFP2+MOkO2cfpvUFuV3hjoKea3+wgnGXb85pvm1IAnD6EfBo0nI891FaHHcyPvfMlabEUI/TAYbOsx43HTy6SMZK8yhF4Ysr1yhRG2e/4ZooclccKNUiH0waD9ryT7X5AKlMSJvEqH0AMD968qcnqZIWJmQtLpleklZo+Ogxk2k9w3zV4Tk+iVDUmi7wti5weHjJBxzckVEB5oqcbmgri2QRubhOrAveOiidUNOu9cy69O2vvnAW9z6C5Aq8UN1gRIeSa5SWjsmHf+LjG9SAelFw3bszqqZ5XYokkdi81BO+U9sdPdnhtPj2udRH67xfaIbLgOSusZ9tKnoGBEe5gVQ52CFZSsM2hvWJPrRqRCPdASc250GIky7DgTal3jHSpOzHLVYdTJkI2thlkc0TmR8JncOoxB6UtXIn6KdvEKQ8SSp7tbInZhyS99we4k0EFNcrTBtmgt0OKS6qF3QekZA+4vqvMwox1hQ90RK8dF148jzYM2K71pNHeK2QUai2gdFj+1KAMuqR57FhQ796VN10kmjWion6ohs/GGSDKYLQt0O367mJZ3vSjxu55PC49HzzdD26hP6rrr5frey29vxr8/Pns5vSmuF5MStNHZdPyyKIE5e3aHyPktEE8qeLzInl3Mp/PFk/XvXjx9+uzR5p/lx22/+Wgzv/7j8hJvi8Xydsq4ZdI4bqx0Qju9HTTPNwP9tre14b6WF4vJ9Z0ufTleFbOL948z/nz2xb1dLB9nKns1X2TzWTHK9OZ/vpyv3jyffb1Ru8fZs/UTPylf5vm70kBeZJNldjWZ/T93n29eXuUv4x9K6ePpxc16mvoyW70pssvJq1fForx2kY1nl9m95ZRIv8/Gl5fLbLLKVvN9geVzTy42iNYN2tsA4TH6Hz2zSx/KqKEgK+93Df5GQSbFsqot9/MGwGnyskJmrqPTvfnjldnyt5MjdzsTwhcU9Auyupr7kCe0HZ5Qhjyh54Ki7qAPvp6kv1HdOrK+wwU9D8h1+MT2BwjqGOMxH1rcu/n8snYoJsVcL+blH+tmknPCj5er0uHVTngXyBhNd5BJzw9gPvxrVyGvXRz8tddPvyAydPB28YHKy+FuF41vBKAns5TJQw2YfeDlB4wQI2duMzDLlzwBleHYyb5jd36KCajN2Nldu4IGMUWzUuyg/oET5X06qP/s5Af1jMyNQFQt81RbMBVtbO4DB8wHPYMLG2TMqcgzYhc0JkGzlD01y6c/C7MkLaZ7hqn9o3hJtFjV6QqD0GKM2AimMoqWeEeSckeACbQTcFeT2aOr8Q8ftZFqo1bKjca1ifwB1/b9y/n8H+sHuf/kdhfWhYwzz2e/ud3I7RJvo2w+m77PpsVqNZm9zlZvFvOb12+y27tfZu/eTC7eZONFkV0vimX5Isuv71Nqz2ef36zezBfZzewfs/m72YdKsZG20Xqb5smdirGNbnJFa5uq29TWv5ImKbd2sJVzzjx76yZBa8WryKnW8d/vthF574vpdP6uemfVNOU7kRISWarrqvYe9b1Ahb6897V3uH1oDQm8eD+ugsH4lukwkKDryewf9dphEaqJOm0LtRGZbCTZyKlt5OV0fAEbSf2hI3H+BRQ46+2JI3fiZ76fRUc9kgtYwVpIYiIfnO/8ICwQPe/Xcpx2LXtdrcgt2xEyili8pXBAeWRAP0xSkdxoH+ow6EmVth1VZVcOtdgLVw7x4Vj7kbozeYrWDbkjASqnrWSMmCuE4y97h39TY7Vf9MpL7KXoYss3fDQOB2IsMZgt4dVeYxiEqnYBZGj7MTwNZd4TlHtej+3JnUUQ9yRls7z5hNL/S9/JP4lNrmqF1Qi/HabN7Zzz/7vepE8ny1X20Ww+O/9fxWJOI5HzrvmaOpwins1XiSa+1yvNEgU2eArMnpoCu5yvHoBaEWRPwTeLw/DN+jR8Mxd5nkcyuEj2di6V0CyWrbFIFiYZZ3Fsi0WyqCj2xDoaUzxiWqPENHWDq9mHQ3AcqXU4a9/7AIxG+x6XyGjiFLX+gEirX3y43KZvwAa0v2LUHVI84lvzD4bbOpLlH+bkgpiOh5PTWqaTC+QIca/j3AFQNBhXVXXViZH0vXCAgCLzTVGIZZ0oR1LzXE8HSKiS3HMi2FxY7v2hh4Sm8Y26K98YpsrtfOMv1xuSLnwjOyXfWLwu15O3RSIb9XaMQSIbU75dIhsPSjYql8jGRDYOkGxUhyIbq8tXyp2sHfkRng7rj5X9TCMtz8KktOYDMkkUgpLHy4J1vTNNcZp+ZkfKcNOHYgW3PYLTiU68ExySV6X5am9u3agL/2+6O+9EPCIslY6YGOe65sW5SAmxNvGW+Ok7SEySicg4xGPFsjHiMezG6YmOd3QesTNlAPH45eRqstosNeW//z4uhSxrOcTs6qa8sZdF9nJevtLxLPsoz+aLjH182HL6nzlVuT3ZsjJRlYmqTFTlAalK/UEbWyRb6x1DmejJXuRC0kLhynrFE5t1aJbyuBmRlTJOyxPxfLBUN4XmPMZiL1Xv8BUnmdBzmEzXg2UwVuMW3u8U1E96RVRyb456DEeLcooVL5snTjFeMmPPSEPVE5g/6GTHD4tT3Fq2UT3kFO+IO2IDzs6zbnpBKfrKr3/mtKJNtGIqt0604nHKrfNEKyZaMWU9BmY92g+HfDpRifWhCEV9MELRfTDExQddO6sOle9YXdr4ABs7NrBKEAvYsaBdo806aayES6xEOCuhIpZg2q4lmDZSbXWe6Ei6WwV6+BIN219bTSSfXEfyKezGyZW0EPkk6+Seb2bAbIXfUUQIk/MTjwSSN1veaJe0GV+sk/S+/6nfIIlYY5SHax1aPb9unbDTozfCW97Ij/8/hWX0zw==