Factorio Forums

www.factorio.com
https://forums.factorio.com/

Accurate belt segment measurements

https://forums.factorio.com/viewtopic.php?f=5&t=70055

Page 1 of 1

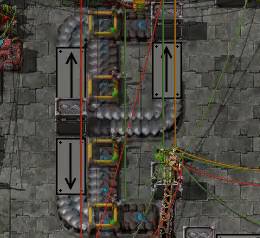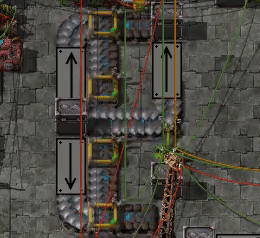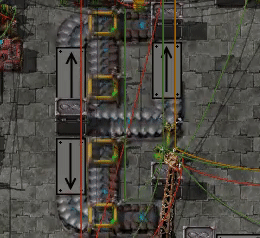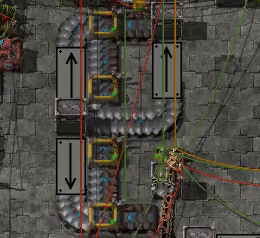
Accurate belt segment measurements

Posted: Sat Apr 27, 2019 3:48 pm
by ignatio
I found myself wondering exactly how long belt segments are, or more precisely how long it takes for an item to get from one end to the other.

The wiki page (as of the time of this posting) tells us that straight segments have 32 "slots", which are travelled 1 slot per tick on a yellow belt, hence it takes 32 ticks from one end to the other. (The page also tells us items take up 9 slots, which is no longer accurate in 0.17, but this is not about that bit of stale info.)

The length of a straight is correct. But then the page describes turns, and says the outer lane of a turn is 37 slots and the inner lane is alternating between 13 and 14 slots, and I couldn't get it to work like that: I did some spirals with turns in only one direction, and cancelling out the straights I got that the successive inner turns took:

13, 13, 13, 14, 13, 13, 13, 14, 13, 13, 13, ...

I.e. only every 4th turn takes 14 ticks, or, put differently, an inner turn seems to be 13.25 slots long. Outer turns too don't quite take 37 ticks each:

36, 37, 37, 37, 37, 37, 37, 37, 36, 37, 37, ...

First I thought that was some off-by-one problem in my test rigs, but it's perfectly repeatable.

Now I got intrigued, so I set up circular belts of different sorts where single items go round and round. Then I added some circuitry to predict the lap times - when the constants are right it should line up perfectly with the real measurements regardless how many laps it takes for the cycle to repeat.

Image

With some deductions from the lap times of those circuits we can measure the fractional slots for each type of belt segment, also including sideloaded belts, underground belts, splitters, etc. I included some sanity checks too, like checking that left and right turns take the same time.

Rather than dealing with fractional "slots" we can scale things up to whole numbers, and so we find that there are in fact 8 times more positions:
  • Straight segments have 256 positions per lane.
  • Yellow belts move items at 8 positions per tick, red 2*8=16, and blue 3*8=24 positions/tick.
  • Underground segments and splitters also have 256 positions per lane.
  • The outer lanes in turns have 295 positions.
  • The inner lanes in turns have 106 positions.
  • Straights and underground entrances sideloaded "early" have 188 positions.
  • Straights and underground exits sideloaded "late" have 68 positions.
With "early" and "late" sideloading above I mean where on the belt the sideloaded items enter - "early" means it's closer to the back (also the only place that isn't blocked on an underground entrance), and "late" means it's closer to the front (and the only place open on an underground exit).

An observation is that it's possible to get items to travel faster by converting inner turns to sideloaded segments. However it doesn't affect the throughput, i.e. items per second.

Based on these findings I'm going to update the wiki page, and also fix the stale item size info at the same time. But I thought to post here first in case there are thoughts on this.

If you want to try it out yourself I've attached the blueprint below. It requires that the infinity chest is unlocked, which you can do with the Creative Items mod, but other than that it should work on vanilla. The test is enabled by turning on the constant combinator in the top left corner. Because I'm a bit lazy with the combinator logic, the speakers will alert when the test is turned on or off, but once that has died down after the start there should be no more alerts as long as it's kept running.

Re: Accurate belt segment measurements

Posted: Sat Apr 27, 2019 3:57 pm
by Bilka
Do you think the "amount of slots" info is important? I was planning to nuke that wiki page....

Re: Accurate belt segment measurements

Posted: Sat Apr 27, 2019 4:14 pm
by ignatio
Well, I think it's interesting to understand the belt mechanics more deeply.

In "normal" gameplay it's arguably not of much practical value, but then again people are doing all sorts of cool things in Factorio that isn't "normal" gameplay, and then it might be useful.

The reason I got into it was that I wanted to have good figures on inserter throughput, and there it turns out that the exact positions of items on the belt wrt the hand can have long-lasting effects. So I need to accurately control the phase between belt items and inserter hands to get good measurements, and then this matters.

Re: Accurate belt segment measurements

Posted: Sat Apr 27, 2019 5:24 pm
by Bilka
ignatio wrote: ↑Sat Apr 27, 2019 4:14 pm Well, I think it's interesting to understand the belt mechanics more deeply.
So it's a typical wiki thing... :roll: I'll figure something out for the page, thanks for the updated data :lol:

Re: Accurate belt segment measurements

Posted: Sat Apr 27, 2019 7:04 pm
by ignatio
It wasn't only out of idle curiosity, although that is a perfectly sufficient reason in my book. ;)

Just to give an example of why belt positions can matter, in these two cases the only difference is that the bottom lane has started one tick later (both inserters use max stack size). The inserter on the left has 36% more throughput than the one on the right, and that's sustained - it never gets better (unless there are gaps on the belt, and if there are it can just as well get worse again).

9.47 items/second: Image 6.92 items per second: Image

What do you have in mind for the wiki page? I'm happy to have a go at it myself.

Re: Accurate belt segment measurements

Posted: Wed May 01, 2019 9:04 am
by Bilka
I missed your question about the wiki page. Good thing I did, because your update to the page turned out amazing. Thank you!

Re: Accurate belt segment measurements

Posted: Wed May 01, 2019 9:55 pm
by ignatio
Cool, I'm glad it's appreciated! :)

Re: Accurate belt segment measurements

Posted: Thu May 02, 2019 4:48 am
by JCav
In your .gif examples, how would one make sure they have the best throughput every time? In other words, how would one start the inserter at the appropriate time to ensure the throughput is highest?

Re: Accurate belt segment measurements

Posted: Thu May 02, 2019 11:59 am
by ignatio
In other words, how would one start the inserter at the appropriate time to ensure the throughput is highest?
That's a good question. It might be possible to sense the items on a belt tile before the inserter and use a few combinators to start the inserter at the right moment.

However a problem with that is that you can only sense belt items with the resolution of one game tick, and that might not be enough. As my belt loop experiment shows, an item can be in any of 24 different positions on an express belt and still register in the same game tick, and the inserter does not react the same way to all those 24 positions.

It's possible to get the resolution down to 8 positions by either measuring over a longer time and detecting the 2-3-3-2-3-3 tick pattern that the express belt produces, or weighing together measurements from several belt tiles. But then the combinator logic starts to get complicated, and the resolution is still only 8 positions which may not be enough. But I don't know that - I have only measured inserter throughputs at 8 position offsets (i.e. for two lanes, 8*8 = 64 measurements (I can explain further where that comes from, but maybe another time because I'm already nested two parenthesis levels here)).

All that makes it a rather complicated and fragile approach. I think it's more practical to just not count on any better throughput than the worst, and instead focus on changing the belt layout to get better throughput.

E.g. the particular case I showed is with items in both lanes, and a turn facing away from the inserter. If it's a straight instead, or - even better - just one lane is in use, then the lowest throughput is much higher: 10.58 items/s in the first case (straight, both lanes), and 11.25 items/s in the 2nd (single lane, but still the same kind of turn).

Yes, that's right - throughput is better if only a single lane is used. That's because the inserter spends less time moving around the hand trying to catch items, and instead more waiting in more or less the same spot for items to arrive. For the quick express belts the latter wins, but the situation gets different for the basic yellow belts. Then the throughput of the belt becomes the limiting factor, i.e. a green stack inserter can empty both lanes of a yellow belt quickly enough.

Re: Accurate belt segment measurements

Posted: Sun Dec 11, 2022 5:16 am
by Nidan
Inserters to belts behavior depends on belt orientation and it being fixed in 1.1.73 prompted me to do some extensive inserter to belt testing. While I can confirm there are no longer orientation based inconsistencies, some results still strike me as odd.

Inserter drop positions (slots until the beginning of the next belt)
For measuring, I'm making use of the results above: A yellow belt moves items 8 slots per tick, a straight belt is 256 slots long and a outer lane of a curve is 295 slots long. So curves shift items by one slot backwards compared to belt speed (295 % 8 == 7) while straight belts don't affect the result (256 % 8 == 0). Thus, with an arrangement of 8 curved belts we can figure out the exact slot from the 8 possibilities we get from just measuring straight belts.

The results are identical across all inserter types.
  • Straight belt
    • From behind: 77
    • From side: 128
    • From front: 179
  • Curved belt
    • On inner lane: 53
    • On outer lane: 147
  • Underground entry
    • From behind or side: 136
    • From front: 179
  • Underground exit
    • From behind: 77
    • From side or front: 127
  • Splitter
    • From behind: 26
    • From side: 47
    • From front: 64
Straight and curved belts are pretty consistent: The item is dropped in the middle of the lane for all curves and for straights when inserting from the side. When inserting from the front or behind, both directions have the same offset from the center, 51 slots. Putting items onto the unobstructed part of an underground belt has the same offset as the straight belt in that situation. Putting items onto the obstructed part seems inconsistent, I'd expect the same offset form the center instead of 8 and -1. Now splitters… Inserting items into a splitter moves them quite a bit forward, 51, 81 or 115 slots ahead compared to the position on a straight belt. According to boskid, splitters have an internal buffer of 51 slots, but I'd only expect the buffer to be used when the splitter can't output items, considering that when items are just flowing through a splitter, they have the same speed as a straight belt.

Inserter swing times (ticks of a complete inserter swing)
Since I was already measuring the tick an inserter drops the first item, adding a bit of circuitry to make the inserter swing twice and measuring the time seemed simple…
Take the base time and ALL modifiers with matching condition.
  • Base swing times (dropping one item on any belt):
    • Burner: 100
    • Yellow: 72
    • Long: 50
    • Fast and Stack: 26
  • Exactly two items: +1
  • At least three items: +8 / +4 / +2 2/3 per item above 2 (rounded down), depending on belt speed. These match the time needed for the belt to move 64 slots (the size of one item).
  • At least three items onto an underground entry from behind or side: +1
  • Splitter from side:
    • Exactly three items: -6 / -2 / ±0, depending on belt speed
    • At least four items: -6 / -3 / -1, depending on belt speed. -2 for blue belts if items % 3 == 2 (5, 8, 11, …)
  • Yellow splitter from front:
    • Exactly three or four items: -4
    • Exactly five or six items: -(items + 1)
    • At least seven items: -8
  • Blue splitter from front:
    • Exactly four items: -1
    • At least five items: -2. -3 if items % 3 == 1 (7, 10, 13, …)
Since inserters can drop into any gap even if it doesn't fit a whole item, once the belt moved once, the inserter can probably see the gap behind the first item. No idea why the extra tick from the second item no longer counts when dropping three or more items. Likewise, no idea why the underground entry takes an extra tick in those situations, could be that extra tick from the second item reappearing. Splitters… are just strange, I have no idea how to explain why they're faster by that specific amount; for being faster in general their internal buffer is probably playing a role. The varying times for blue belts look like an artifact of the belt speed.
All times are UTC
Page 1 of 1

Powered by phpBB® Forum Software © phpBB Limited