Accumulator / Solar panel ratio
Posted: Fri Aug 29, 2014 2:03 pm
Hello everyone.
I was thinking about the energy model of factory, when i decided to look over the internet what people were actually doing. I found a nice design from Cellidor on reddit. Using blueprint and roboports for solar panel farms is especially nice since it allow you to scale the energy production very fast to match the huge consumption that using productivity modules implies. Otherwise it's a lot more time invested in the building of those, and you spend much more time placing solar panels than doing anything else. Moreover, it allow your solar panel farm to be a safe way for drones. Space is generally not the rarest resource in factorio.
However, I was not happy with the solar panel / accumulator ratio in this design. Without good reason at first, only a disturbing feeling. I decided to resolve the question of the ratio a bit more rationally. This is what i will explain below. Please tell me if i've done any error, i'm very interested in this.
edit: As pointed out by ssilk, this question has already been discussed several times. A list of forum topics discussing about this can be found on the wiki page for solar panels.
How to compute the optimal Accumulator / Solar panel ratio.
Let's say that our factory is using an average power P and that we want to power it only with solar panels and accumulators. Since solar panel are the only outpur of electricity, they need to generate during a whole day enough energy E_sol to provide an average power P during this time. . Let's note t1 the day time, t2 the night time and t3 the dawn or dusk time which are the same and T = t1+t2+2*t3 a whole day time. The energy E_sol is :
E_sol = P * T = P * (t1 + t2 + 2 * t3)
Since the daylight allows them to produce electricity only during a fraction of a day, they need to provide an output power P' greater than P to not only power the factory during the day but also charge the accumulators which will power it during the night. The energy produced during a day by the solar panel is the sum of the power outputed on each game tick and can be computed as the area of the trapezoid described by the solar panel power curve, represented in red below.

This trapezoid has height P' and sides t1 and t1+ 2 * t3. Thus we can also define E_sol as
E_sol = P' * (t1 + t1 + 2*t3) / 2 = P' * (t1 + t3)
Using the two previous equations we have
E_sol = P * T = P' * (t1 + t3)
frow what we can compute P' as
P' = P * T / (t1 + t3)
The capacity storage needed for the accumulator to maintain the output power P during dusk, night and dawn (represented as a blue curve above) can also be calculated as the area of the trapezoid below the accumulator power curve. This trapezoid has height P but its sides needs to be calculated. The accumulators starts to output power when the solar panels output falls below P. Since their output power falls linearly from P' to 0 in time t3, the time during which the accumulator output is growing is t3 * P/P'. Thus we have that the energy E_acc restored during the night is
E_acc = P * (t2 + t2 + 2 * (t3 * P/P')) / 2 = P * (t2 + t3*P/P')
Now, say we want to compute then number of accumulators n and the number of solar panels m needed to provide the target power P at any time. They can be computed from the capacity c of one accumulator and the power output o of one solar panel.
n = E_acc / c
m = P' / o
Finally, the ratio of these two values can be computed :
n / m = (E_acc / P') * (o / c) = [(t1 + t3) * [t2 + t3 * (t1 + t3) / T] / T] * (o/c)
We can get the values from the wiki.
o = 60 kW
c = 5000 kJ
t1 = 0.5
t2 = 0.1
t3 = 0.2
T = 1.0
Times are in fraction of day, so they must be multiplied by (25 000 / 60). With these numbers, the numerical application gives us :
n / m = [(0.5 + 0.2) * [0.1 + 0.2*((0.5+0.2) / 1.0] / 1.0] * (25 000 / 60) * (60 / 5000) = 0.84
It does mean that for 100 solar panels, we need 84 accumulators.
Some remarks about this result.
Exploitation of the result.
A possible exploitation of this result is to define a building pattern for solar panel and accumulators in which the ratio is preserved. Thus, each time the pattern is built, the ratio stay the same.
Here is an example of pattern. It uses roboport on the center so its repetition (with up to two tiles between each pattern, allowing to move between them) is possible and can be built by construction robots automatically. It as a space efficiency of 96.5% (3.5% of the tiles, used by the roboport and the substations, are not used by solar panel and/or accumulators) and an accumulator/solar panel ratio of 0.84.
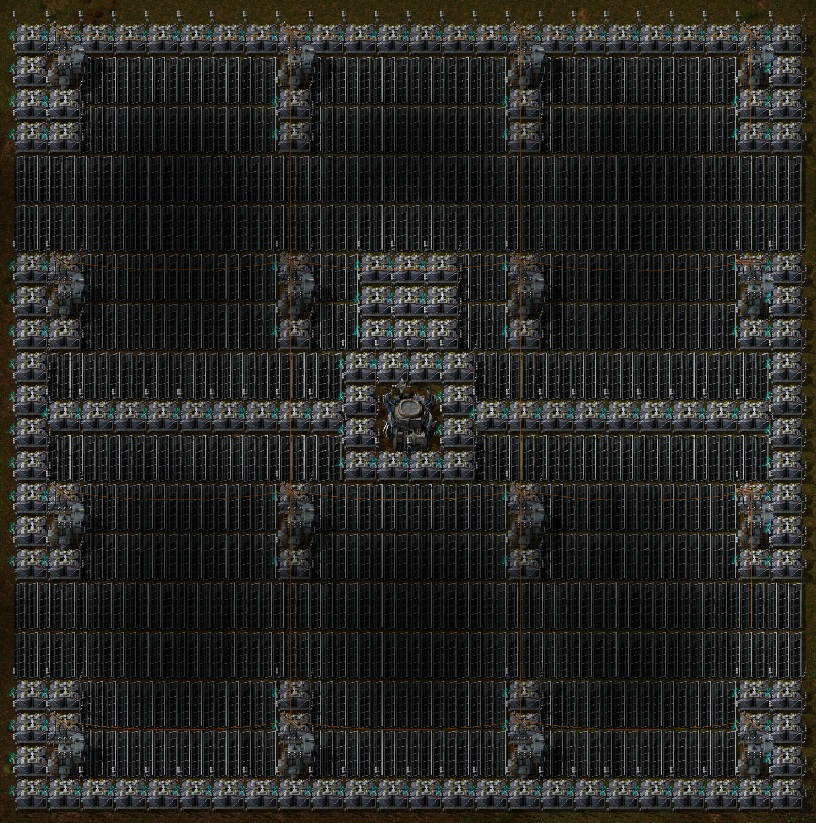
Size: 48x48 (2304 tiles)
Usefull area : 2224 (96.5%)
Solar panels: 180
Accumulators: 151
Substations: 16
Roboport: 1
* Logistic network tilable
* Electric network tilable
I was thinking about the energy model of factory, when i decided to look over the internet what people were actually doing. I found a nice design from Cellidor on reddit. Using blueprint and roboports for solar panel farms is especially nice since it allow you to scale the energy production very fast to match the huge consumption that using productivity modules implies. Otherwise it's a lot more time invested in the building of those, and you spend much more time placing solar panels than doing anything else. Moreover, it allow your solar panel farm to be a safe way for drones. Space is generally not the rarest resource in factorio.
However, I was not happy with the solar panel / accumulator ratio in this design. Without good reason at first, only a disturbing feeling. I decided to resolve the question of the ratio a bit more rationally. This is what i will explain below. Please tell me if i've done any error, i'm very interested in this.
edit: As pointed out by ssilk, this question has already been discussed several times. A list of forum topics discussing about this can be found on the wiki page for solar panels.
How to compute the optimal Accumulator / Solar panel ratio.
Let's say that our factory is using an average power P and that we want to power it only with solar panels and accumulators. Since solar panel are the only outpur of electricity, they need to generate during a whole day enough energy E_sol to provide an average power P during this time. . Let's note t1 the day time, t2 the night time and t3 the dawn or dusk time which are the same and T = t1+t2+2*t3 a whole day time. The energy E_sol is :
E_sol = P * T = P * (t1 + t2 + 2 * t3)
Since the daylight allows them to produce electricity only during a fraction of a day, they need to provide an output power P' greater than P to not only power the factory during the day but also charge the accumulators which will power it during the night. The energy produced during a day by the solar panel is the sum of the power outputed on each game tick and can be computed as the area of the trapezoid described by the solar panel power curve, represented in red below.

This trapezoid has height P' and sides t1 and t1+ 2 * t3. Thus we can also define E_sol as
E_sol = P' * (t1 + t1 + 2*t3) / 2 = P' * (t1 + t3)
Using the two previous equations we have
E_sol = P * T = P' * (t1 + t3)
frow what we can compute P' as
P' = P * T / (t1 + t3)
The capacity storage needed for the accumulator to maintain the output power P during dusk, night and dawn (represented as a blue curve above) can also be calculated as the area of the trapezoid below the accumulator power curve. This trapezoid has height P but its sides needs to be calculated. The accumulators starts to output power when the solar panels output falls below P. Since their output power falls linearly from P' to 0 in time t3, the time during which the accumulator output is growing is t3 * P/P'. Thus we have that the energy E_acc restored during the night is
E_acc = P * (t2 + t2 + 2 * (t3 * P/P')) / 2 = P * (t2 + t3*P/P')
Now, say we want to compute then number of accumulators n and the number of solar panels m needed to provide the target power P at any time. They can be computed from the capacity c of one accumulator and the power output o of one solar panel.
n = E_acc / c
m = P' / o
Finally, the ratio of these two values can be computed :
n / m = (E_acc / P') * (o / c) = [(t1 + t3) * [t2 + t3 * (t1 + t3) / T] / T] * (o/c)
We can get the values from the wiki.
o = 60 kW
c = 5000 kJ
t1 = 0.5
t2 = 0.1
t3 = 0.2
T = 1.0
Times are in fraction of day, so they must be multiplied by (25 000 / 60). With these numbers, the numerical application gives us :
n / m = [(0.5 + 0.2) * [0.1 + 0.2*((0.5+0.2) / 1.0] / 1.0] * (25 000 / 60) * (60 / 5000) = 0.84
It does mean that for 100 solar panels, we need 84 accumulators.
Some remarks about this result.
- This result only apply when solar energy is the only source of electricity production. Otherwise, other sources of electricity production will have the priority on accumulators. In this case, accumulator can provide a temporary increase in power when needed (for instance for laser turret during an alien attack) and their number is not calculated this way and generally much lower.
- During the night, the energy consumption is generally a bit higher since lights are turned on. However, the power consumption from light is generally too small to change this result significantly.
- In general, we build more solar panel than needed to ensure that at any moment, we can provide all the required power. However, I have assumed in my calculation that we had built the exact number of each structure necessary, not one more, not one less. However, the result is relevant in any case. If you don't use this ratio, and if your needs of energy are growing, one of this two situation will eventually happen : either your ratio is below 1.05 and you wont have enough energy stored for the night, or, your ratio is above and you wont be able to fill your accumulators during the day.
- We consider here an average power P needed. In general, there may be important variations of the power consumption. We can probably safely use the average power for the following reasons. During the day, the output power P' is usually enough (42% higher than P) to fill any power requirement. If it's not enough, accumulators can probably fill the difference. The variations of the consumption above and below P will be compensated by the accumulators which will charger slower or faster. (This is the purpose of accumulatrs) During the night, if there is a consumption pick, accumulators have a much higher maximum output power than what they are outputing on average, thus it's very unlikely there will be power shortage.
Exploitation of the result.
A possible exploitation of this result is to define a building pattern for solar panel and accumulators in which the ratio is preserved. Thus, each time the pattern is built, the ratio stay the same.
Here is an example of pattern. It uses roboport on the center so its repetition (with up to two tiles between each pattern, allowing to move between them) is possible and can be built by construction robots automatically. It as a space efficiency of 96.5% (3.5% of the tiles, used by the roboport and the substations, are not used by solar panel and/or accumulators) and an accumulator/solar panel ratio of 0.84.

Size: 48x48 (2304 tiles)
Usefull area : 2224 (96.5%)
Solar panels: 180
Accumulators: 151
Substations: 16
Roboport: 1
* Logistic network tilable
* Electric network tilable