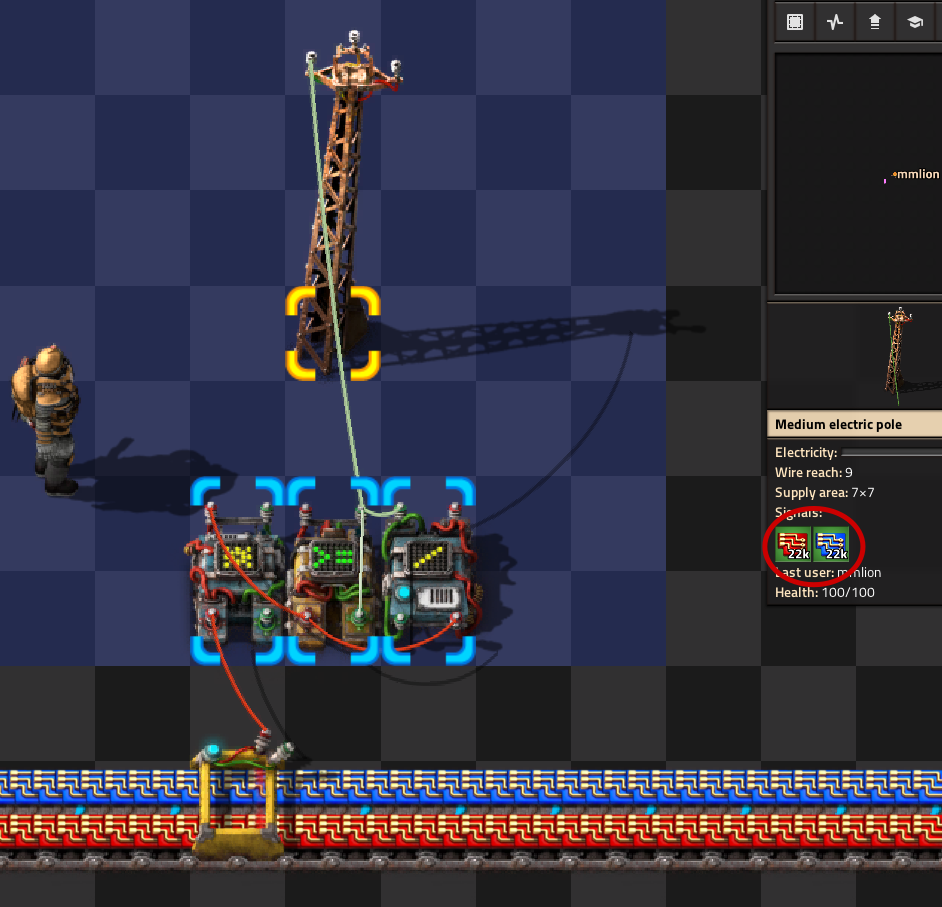
Kalman filter for simple average belt flow measurement
Posted: Mon Jan 10, 2022 5:58 pm
I'd like to share a very compact design to measure a belt flow. I know that there is a way to measure the flow by connecting 100 belts in a line together, but it is too heavy in my opinion. Here is another simple solution.
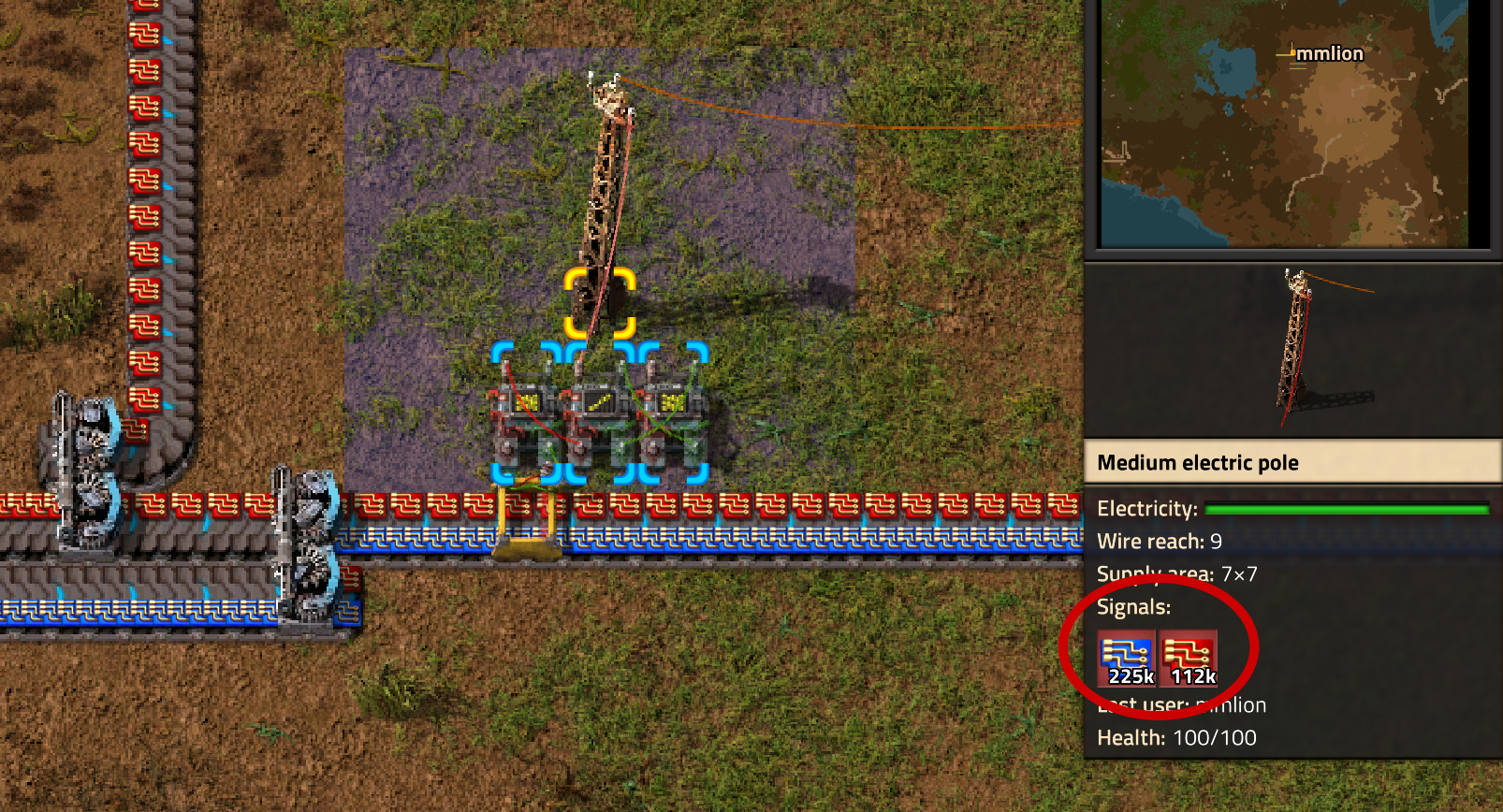
On the picture 225k and 112k means that the average flow is equal to 22.5 and 11.2 items per second.
The main idea is to use the simplified Kalman filter: if f_n denotes the instant flow speed at tick n, then prediction of the average flow is
where a is a constant between 0 and 1, which controls duration of the filter's reaction to the changes. For example, if representative measurement time is 3 sec = 180 tick, and computation takes 2 ticks, then a=1/90.
The instant flow speed f_n is equal to the number I_n of items on a belt multiplied by 45/8 (for express belts). I also decided to multiply I_n by 10000 due to integer computations in factorio. So
Unfortunately, integer computations gives a small error at the end (for example, a fully compressed belt leads to the value 449k instead of 450k), so it is better to rise 56250 a little and have a nice round numbers like 450k. So, I used the following formulae for normal/fast/express belts:
If prolonged duration of filter's reaction is needed, numbers (89,90) can be substituted by (299,300) (for 10 seconds representative reaction time), or any other pair (N-1,N).
I'm interested if this design seems interesting/usable.
On the picture 225k and 112k means that the average flow is equal to 22.5 and 11.2 items per second.

The main idea is to use the simplified Kalman filter: if f_n denotes the instant flow speed at tick n, then prediction of the average flow is
Code: Select all
K_(n+1) = a * f_n + (1-a) * K_nThe instant flow speed f_n is equal to the number I_n of items on a belt multiplied by 45/8 (for express belts). I also decided to multiply I_n by 10000 due to integer computations in factorio. So
Code: Select all
F_(n+1) = ( (10000*45/8) * I_n + 89 * F_n ) / 90 = ( 56250 * I_n + 89 * F_n) / 90
Code: Select all
F_(n+1) = ( 18800 * I_n + 89 * F_n) / 90 (normal)
F_(n+1) = ( 37500 * I_n + 89 * F_n) / 90 (fast)
F_(n+1) = ( 56300 * I_n + 89 * F_n) / 90 (express)
I'm interested if this design seems interesting/usable.