Page 1 of 2
On the capacity of trains
Posted: Sun May 06, 2018 12:18 am
by jcranmer
I don't think anyone has pounded out the theorycrafting, so let me have a go at it.
The question to ask here is a deceptively simple one:
what is the capacity of a rail network? Trying to find information on this topic is difficult, since most theorycrafting works on belts and bots, and the underlying formulas for trains aren't easy to track down.
Step 0: How to tackle the question
Trains are complex, and so the answer to how much can you move by rail is going to have to have a complex answer. It's going to need to be answered in several parts. Breaking it down into pieces, we need to start by looking at what the absolute maximum throughput of a rail is, in terms of all trains infinitely remaining at the same speed on a track. Then, we can look at the impact of getting trains to and from their max speed. At that point, we can observe the impact of stations on throughput. Finally, we can integrate the impact of more complex train networks and switching on capacity. But before we can quantify anything, we need to understand first how trains work.
In terms of formulas, trains have more formulas that you need to know than any other logistic system. There are distinct formulas for acceleration, deceleration, and braking distance that are critical to analysis, not to mention the basic calculations for computing things like maximum speed, energy consumption, train loading, etc. Here are the formulas I have:
- Acceleration: speed at next tick = (speed - min(speed, friction / weight) + power / weight) * (1 - air_resistance / weight) {up to max_speed}
- Braking distance (in tiles): max( ½ * weight * speed / (braking + friction), 1.1) * speed + 2
Values used in these (and subsequent) formulas:
- speed: Speed in tiles/tick. Max speed of a nuclear fuel train (298.1km/h) is 1.38. Note that the speed in the GUI is shown as km/h, divide by 216 to get tiles/tick.
- friction: Sum of all friction_force values on the locomotives and wagons on the train. This is 0.5 each for locomotive and wagon.
- weight: Sum of all weight values on the locomotives and wagons on the train. This is 2000 for locomotives and 1000 for wagons.
- power: I'm not entirely sure where this value comes from, but this is where I believe the fuel acceleration modifiers kick in, and it's dependent on the number of forward-facing locomotives.
- air_resistance: The air_resistance value of the first thing in the train. 0.075 for locomotives, 0.01 for wagons.
- braking: Sum of all braking_force values on the locomotives and wagons on the train, multiplied by the braking force bonus modifier. This is 10 for locomotives and 3 for wagons, assuming +0% braking force.
Okay, let's get into the math now.
Step 1: Assume trains at constant speed on an infinite track…
Imagine you had an infinite flat track with trains going at a constant speed spaced several tiles apart. Now imagine a signal on this track. It will start out green. A train will come along, reserve it and change it to yellow when its braking distance spot passes over the signal. Then the train will pass over the signal, and the signal will change to red. When the train passes through the signal, it will stay red until the train passes the next signal some distance away. Then our signal changes back to green, awaiting the next train. If we shrink the length of the green cycle to an infinitesimally small amount, then it is impossible to squeeze any more trains on the track without slowing them down. Thus the capacity of a track is 1 train / (time_yellow + time_red), and is obviously dependent on train length, braking distance, speed, and signal distance.
Let's return to the braking distance formula. If we assume vanilla parameters, we can simplify the equation. One thing that may seem surprising is that braking distance does not depend on train length or train consist details, but rather the ratio of locomotives to wagons:
R = # wagons / # locomotive. A 1-4, 2-8, even a 5-20 train all have the exact same braking distance. Another simplification is the max: for max speed trains, the first leg of the max is going to be in the region of 100. Trains really have to be going very slow for the 1.1 to kick in instead. With that in mind, here is a simplified formula (
B = braking force modifier, i.e., goes from 1 to 2 in vanilla research):
- braking distance (in tiles) = 1000 * (speed)² * (R + 2) / (2 * B * (3R + 10) + R + 1) + 2
- yellow cycle time (in ticks) = braking distance / speed = 1000 * speed * (R + 2) / (2 * B * (3R + 10) + R + 1) + 2 / speed
For comparison, the braking distance of an unladen locomotive with nuclear fuel at max speed is 185 tiles with no braking force research and 95 tiles at max braking force, as experimentally measured (with a long straight line of signals, counting how many signals were yellow at any given point in time), the theoretical calculation is a hair below that 183.3 and 94.9 tiles--within the reliability of measuring via experiment (which can only accurately get within about 2 tiles). For a 1-to-4 ratio train, the theoretical values are 235 and 124 tiles for no and max braking research. A 1-to-10 train needs 135 tiles to brake at max braking research.
A red cycle consists of first the time it takes for the entire train to pass the signal, and then the time for the train to clear the block. The first is (7 * L * R / speed), where L is the number of locomotives, and the second is (signal_distance / speed. Summing up, we get:
- red cycle time = (7 * L * R + signal_distance) / speed
- total time = 1000 * speed * (R + 2) / (2 * B * (3R + 10) + R + 1) + (7 * L * R + signal_distance + 2) / speed
- Throughput (in trains per tick) = 1 / total time
I'd show the full equation for throughput, but it's very messy. Punch it into wolfram alpha or your other favorite CAS if you really want to see it. Instead, let's look at what the formula boils down to if we only vary one variable:
- Throughput per speed = O(1 / speed). Higher max speed means lower throughput. This is actually true to reality, too--higher speed is lower throughput.
- Throughput per braking speed = O(1), O(B) for yellow cycle time only. If you had an infinite braking speed research, the value would reach an asymptote and wouldn't decrease forever. Intuitively, this makes sense: braking speed only decreases the yellow cycle time, so even if you drove it to 0, you'd still have to worry about the red cycle time.
- Throughput per signal distance = O(1), O(D) for red cycle time only. Same thing: drive the signal distance down, and you shrink red cycle time without touching yellow cycle.
- Throughput per locomotive ratio = O(1). Essentially, the makeup of your train doesn't matter in the long run.
- Throughput of total cargo moved = O(k * #cargo wagons / (#cargo wagons + l)), where k and l are some constants. Effectively, there is a maximum capacity you will hit (for 1-to-4 ratios, that maximum capacity is about 11.8 per second), but increasing the number of cargo wagons will get you closer to the asymptote.
At late game research, you're looking at perhaps 1.8 cargo wagons per second for a 1-4 train with signal-every-big-power-pole, and 5.6 cargo wagons per second for a 5-20 train. Essentially, at the scale that's practical for Factorio, train throughput is close to constant, so the best way to improve your capacity is to build longer trains.
When I find more time, I'll come back and discuss the later portions.
Re: On the capacity of trains
Posted: Sun May 06, 2018 12:50 am
by bobucles
It might be easier to attack this problem from a different angle. The maximum, frictionless vacuum throughput of a rail line is pretty easy to calculate:
- Start with a very long train moving at maximum speed across a very long track.
- Pick a point on the track.
- Start a stopwatch and count the exact time X that it takes for Y cargo cars to pass through that point. Ignore the locomotives.
You can probably calculate this "maximum, frictionless vacuum" time using combinators. Rail signals turn red the exact moment that a train enters a block. So you can take this measurement by placing 2 signals 10 train cars apart (70 tiles), start the timer when the first signal turns red, and end the timer when the second signal turns red. It should take about, I dunno, two seconds? I'll use that number as an example.
So you have 10 cargo cars crossing through a point every 2 seconds, or 5 cargo cars per second. Multiply by the total cargo capacity of the car( I will assume we are moving ore, which is 50 items per slot or 2000 ore per car. So:
Code: Select all
5 train cars, moving at maximum speed, carrying 2000 ore each, pass through a rail point in one second.
Using this time estimate the maximum frictionless vacuum throughput of a single rail line is 10000 ore/second or 600000 ore/min. But that's not a very useful metric. Now we need to subtract everything that ISN'T a cargo car moving at maximum speed. So:
- Every tile that isn't occupied by a cargo car costs efficiency. This does include the space occupied by locomotives. It also includes rail signal placement, as moving trains will never compress closer than the distance between your rail signals. This will be different for every train and every network and will be very difficult to fully calculate.
- Every train that isn't moving at 298kph RIGHT NOW costs efficiency. The average throughput will be multiplied by the average speed of the train. Train depots obviously have much lower throughput because trains are stopping and moving at slow speed. Long train highways have fast trains giving high throughput. Clogged intersections have slow moving trains, which cripples the throughput, which causes more trains to back up, which hurts throughput even more! It's a vicious cycle.

Ultimately this will give you a single value: The number of cargo cars flowing through a point per second. You can get an exact measurement of this in game by using standardized train sizes and counting the number of trains that flow through a point. If you get 10 trains a minute and they are 1-3-1 trains, you are moving 1000 ore/second. Pretty simple, right? I think Shredguy99 did a train counter a long time ago but it shouldn't be too difficult to set up. Just count the number of times a signal turns red. As long as trains don't get so close together that they send a single red pulse (is this even possible?), it should work.
Re: On the capacity of trains
Posted: Sun May 06, 2018 1:40 am
by Frightning
The most direct way to compute the theoretical upper bound is to determine max train speed and the corresponding loco-to-wagon ratio required to attain this speed. Then, suppose one had an 'infinitely' long train featuring said ratio. Such a train would travel at the top speed of trains, and hence move wagons at that speed, but only a portion of the train is actually made of wagons. both wagons and locos are exactly 7 tiles long, so you can compute the throughput, in wagons/sec, by taking velocity in tiles/sec, and dividing 7, and then multiplying that answer by the proportion of the train that is wagons (that is, 'wagons/(locos+wagons)'). I don't know the relevant numbers anymore since newer fuels introduced a vehicle acceleration modifier that changes top speed and the ideal ratio, but would interested in seeing the concrete numbers/math for deriving those numbers. (Old max velocity was 1.2 tiles/tick=72 tiles/sec, and exactly 6 locos to 13 wagons -> 13 wagons to 19 7-tile units of train)). Throughput is likely increased by a significant margin over old numbers both because the train is now notably faster, but especially because the loco-to-wagon ratio is now more wagon heavy than before (particularly evident with ideal nuclear fuel with it's 250% vehicle acceleration).
Re: On the capacity of trains
Posted: Sun May 06, 2018 3:00 am
by jcranmer
bobucles wrote:Ultimately this will give you a single value: The number of cargo cars flowing through a point per second. You can get an exact measurement of this in game by using standardized train sizes and counting the number of trains that flow through a point. If you get 10 trains a minute and they are 1-3-1 trains, you are moving 1000 ore/second. Pretty simple, right? I think Shredguy99 did a train counter a long time ago but it shouldn't be too difficult to set up. Just count the number of times a signal turns red. As long as trains don't get so close together that they send a single red pulse (is this even possible?), it should work.
Sure, you can experimentally measure the train capacity. But I'm not interested in how many trains my current network supports, I'm interested in how many trains a perfectly desired network could support. Experimental trial and error is not an efficient means to that end.
Frightning wrote:The most direct way to compute the theoretical upper bound is to determine max train speed and the corresponding loco-to-wagon ratio required to attain this speed. Then, suppose one had an 'infinitely' long train featuring said ratio. Such a train would travel at the top speed of trains, and hence move wagons at that speed, but only a portion of the train is actually made of wagons. both wagons and locos are exactly 7 tiles long, so you can compute the throughput, in wagons/sec, by taking velocity in tiles/sec, and dividing 7, and then multiplying that answer by the proportion of the train that is wagons (that is, 'wagons/(locos+wagons)'). I don't know the relevant numbers anymore since newer fuels introduced a vehicle acceleration modifier that changes top speed and the ideal ratio, but would interested in seeing the concrete numbers/math for deriving those numbers. (Old max velocity was 1.2 tiles/tick=72 tiles/sec, and exactly 6 locos to 13 wagons -> 13 wagons to 19 7-tile units of train)). Throughput is likely increased by a significant margin over old numbers both because the train is now notably faster, but especially because the loco-to-wagon ratio is now more wagon heavy than before (particularly evident with ideal nuclear fuel with it's 250% vehicle acceleration).
Maximum speed is 1.38 tiles/tick, and it's independent of locomotive-to-wagon ratio. (Locomotives dictate acceleration, not max speed). Theoretically, you could get 1.37 / 7 * 60 = 11.83 wagons/second in the limit, but that doesn't exactly dictate what's realistically achievable. The 5/20 trains we've been using on a Clusterio mining server should be pulling about 5-6 wagons/second per lane of track by my calculations, although we're almost certainly too clogged to hit max speed (which may be a good thing, given that lower speeds work better for higher throughput).
It's worth reiterating that higher speed isn't necessarily a good thing: in order to keep higher speeds, you need to have wider spacing between trains. So you can clear spaces faster, but the space you need to clear is longer. In the simplistic measure of throughput as wagons / sec = wagons / tile * tiles / sec, it's more effective to increase your wagon / tile count, since you can do that without decreasing tile / sec, but increasing tile /sec comes with a penalty to wagons / tile.
Re: On the capacity of trains
Posted: Sun May 06, 2018 4:17 am
by Zavian
Personally I think theoretical calculation of max rail throughput on an infinitely long rail-line without junctions aren't very interesting. In practice almost very rail-line needs junctions. If you have a good multi lane junction design, then you can often increase rail-line throughput by adding additional tracks. In practice, that increase isn't linear, and is normally bottlenecked by your junction performance, so detailed knowledge of maximum theoretical single track throughput isn't really relevant to considering actual throughput in most actual in game situations. What is relevant is junction throughput. The best reference to that is
viewtopic.php?f=194&t=46855.
Re: On the capacity of trains
Posted: Sun May 06, 2018 7:47 am
by Lubricus
I agree on that the junctions usually is the bottleneck.
With a perfect rail-network without crossings I suppose the inserters loading and unloading trains is the bottleneck, but that depends on how many station you cram onto a rail (is it possible with several train-stations without crossings?).
Re: On the capacity of trains
Posted: Sun May 06, 2018 7:59 am
by Frightning
jcranmer wrote:bobucles wrote:Ultimately this will give you a single value: The number of cargo cars flowing through a point per second. You can get an exact measurement of this in game by using standardized train sizes and counting the number of trains that flow through a point. If you get 10 trains a minute and they are 1-3-1 trains, you are moving 1000 ore/second. Pretty simple, right? I think Shredguy99 did a train counter a long time ago but it shouldn't be too difficult to set up. Just count the number of times a signal turns red. As long as trains don't get so close together that they send a single red pulse (is this even possible?), it should work.
Sure, you can experimentally measure the train capacity. But I'm not interested in how many trains my current network supports, I'm interested in how many trains a perfectly desired network could support. Experimental trial and error is not an efficient means to that end.
Frightning wrote:The most direct way to compute the theoretical upper bound is to determine max train speed and the corresponding loco-to-wagon ratio required to attain this speed. Then, suppose one had an 'infinitely' long train featuring said ratio. Such a train would travel at the top speed of trains, and hence move wagons at that speed, but only a portion of the train is actually made of wagons. both wagons and locos are exactly 7 tiles long, so you can compute the throughput, in wagons/sec, by taking velocity in tiles/sec, and dividing 7, and then multiplying that answer by the proportion of the train that is wagons (that is, 'wagons/(locos+wagons)'). I don't know the relevant numbers anymore since newer fuels introduced a vehicle acceleration modifier that changes top speed and the ideal ratio, but would interested in seeing the concrete numbers/math for deriving those numbers. (Old max velocity was 1.2 tiles/tick=72 tiles/sec, and exactly 6 locos to 13 wagons -> 13 wagons to 19 7-tile units of train)). Throughput is likely increased by a significant margin over old numbers both because the train is now notably faster, but especially because the loco-to-wagon ratio is now more wagon heavy than before (particularly evident with ideal nuclear fuel with it's 250% vehicle acceleration).
Maximum speed is 1.38 tiles/tick, and it's independent of locomotive-to-wagon ratio. (Locomotives dictate acceleration, not max speed). Theoretically, you could get 1.37 / 7 * 60 = 11.83 wagons/second in the limit, but that doesn't exactly dictate what's realistically achievable. The 5/20 trains we've been using on a Clusterio mining server should be pulling about 5-6 wagons/second per lane of track by my calculations, although we're almost certainly too clogged to hit max speed (which may be a good thing, given that lower speeds work better for higher throughput).
It's worth reiterating that higher speed isn't necessarily a good thing: in order to keep higher speeds, you need to have wider spacing between trains. So you can clear spaces faster, but the space you need to clear is longer. In the simplistic measure of throughput as wagons / sec = wagons / tile * tiles / sec, it's more effective to increase your wagon / tile count, since you can do that without decreasing tile / sec, but increasing tile /sec comes with a penalty to wagons / tile.
A train too heavy on wagons cannot travel at the maximum speed for trains, and hence will deliver a lower throughput (so the loco-wagon ratio DOES still matter).
Higher speed is better as any efficiency losses due to following distance can be reduced by longer trains and more frequent signalling (the latter only does so much, but the former can force inefficiency due to train-to-train gap down towards 0 in the limit).
Re: On the capacity of trains
Posted: Sun May 06, 2018 5:30 pm
by bobucles
lower speeds work better for higher throughput).
hhhhhhhowwwwwwww did you come to this conclusion again? Slower things move slower. It's kind of implied. Granted a system that can maintain a slow but steady pace will be far more reliable than a fast system that suddenly gridlocks.
in order to keep higher speeds, you need to have wider spacing between trains. So you can clear spaces faster, but the space you need to clear is longer. In
I'm not sure how true this statement is. Trains do not attempt to enter the next rail block until the train in front totally exits it. By the time the first gap has filled in, the train in front has already moved ahead. The smallest gap between two moving trains is going to be related to the largest gap between two rail blocks. See?
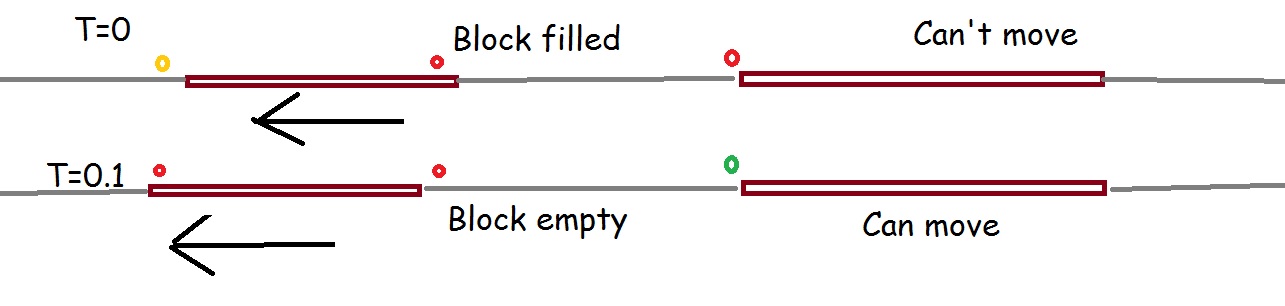
- factorio moving trains.jpg (49.86 KiB) Viewed 8725 times
The best way to pack moving trains closer together is to place the signals closer together. I don't have the exact math for this, but you should try to keep your signals close together at the slowest parts of your train network (depots and junctions). Pick a standardized but not too long distance between signals for your highways.
Re: On the capacity of trains
Posted: Sun May 06, 2018 6:43 pm
by quyxkh
Pretty sure minimum distance between trains is the braking distance, trains try to reserve through the block that contains their current stop point,right?
Re: On the capacity of trains
Posted: Sun May 06, 2018 6:44 pm
by jcranmer
bobucles wrote:lower speeds work better for higher throughput).
hhhhhhhowwwwwwww did you come to this conclusion again? Slower things move slower. It's kind of implied. Granted a system that can maintain a slow but steady pace will be far more reliable than a fast system that suddenly gridlocks.
Did you read my first post? Or did you decide it was a wall of text and you didn't have anything to take away from it?
For a train to move at top speed, it needs to have an empty space in front of it for braking distance (you can see the empty gap if you turn on one of the debug options). When the braking distance hits a red light, the train has to slow down until it can change the light to yellow. That distance grows according to the square of the speed, while the time it takes to clear that distance only grows linearly with speed. Thus, the time interval between trains grows in proportion to train speed.
bobucles wrote:in order to keep higher speeds, you need to have wider spacing between trains. So you can clear spaces faster, but the space you need to clear is longer. In
I'm not sure how true this statement is. Trains do not attempt to enter the next rail block until the train in front totally exits it. By the time the first gap has filled in, the train in front has already moved ahead. The smallest gap between two moving trains is going to be related to the largest gap between two rail blocks. See?
factorio moving trains.jpg
The error in your diagram is that you're not accounting for the yellow signals of the second train, which slows it down.
I honestly don't know why people are so surprised that higher speeds means lower throughput for trains. This is true in Factorio, as can be demonstrated both from theoretical terms as well as experimental terms, and it's true for real life trains.
Re: On the capacity of trains
Posted: Sun May 06, 2018 6:52 pm
by Frightning
jcranmer wrote:bobucles wrote:lower speeds work better for higher throughput).
hhhhhhhowwwwwwww did you come to this conclusion again? Slower things move slower. It's kind of implied. Granted a system that can maintain a slow but steady pace will be far more reliable than a fast system that suddenly gridlocks.
Did you read my first post? Or did you decide it was a wall of text and you didn't have anything to take away from it?
For a train to move at top speed, it needs to have an empty space in front of it for braking distance (you can see the empty gap if you turn on one of the debug options). When the braking distance hits a red light, the train has to slow down until it can change the light to yellow. That distance grows according to the square of the speed, while the time it takes to clear that distance only grows linearly with speed. Thus, the time interval between trains grows in proportion to train speed.
bobucles wrote:in order to keep higher speeds, you need to have wider spacing between trains. So you can clear spaces faster, but the space you need to clear is longer. In
I'm not sure how true this statement is. Trains do not attempt to enter the next rail block until the train in front totally exits it. By the time the first gap has filled in, the train in front has already moved ahead. The smallest gap between two moving trains is going to be related to the largest gap between two rail blocks. See?
factorio moving trains.jpg
The error in your diagram is that you're not accounting for the yellow signals of the second train, which slows it down.
I honestly don't know why people are so surprised that higher speeds means lower throughput for trains. This is true in Factorio, as can be demonstrated both from theoretical terms as well as experimental terms, and it's true for real life trains.
Maybe because train speed must be compared to the 'density' of wagons to realistically compare throughput, just because the train gap has narrowed doesn't mean that you've gained throughput, this is especially true for longer trains, as the gap between 1-2-0 trains is the same as for 10-20-0 trains, at a given speed, hence the larger the trains, the less the gap matters. (Again, why I pointed out that loco-to-wagon ratio that achieves top speed is relevant to computing the upper bound for train throughput, realistically, you won't ever reach said upper bound, but in principle, you can get arbitrarily close to it).
Re: On the capacity of trains
Posted: Sun May 06, 2018 6:53 pm
by Zavian
I believe they reserve their entire braking distance. If we assume trains brake using constant deceleration, then doubling the speed will increase the braking distance by a factor of four. So increasing train speed can actually decrease throughput.
Re: On the capacity of trains
Posted: Sun May 06, 2018 8:02 pm
by Frightning
Zavian wrote:I believe they reserve their entire braking distance. If we assume trains brake using constant deceleration, then doubling the speed will increase the braking distance by a factor of four. So increasing train speed can actually decrease throughput.
For trains of a given length, yes, but one can lengthen the train without changing its braking distance by maintaining the same loco-to-wagon ratio (this is because braking force, and weight are all increased by the same proportion, moreover, the same applies to power and hence the acceleration and top speed are the same for the longer train as they are for the shorter train). Therefore, the effect of braking distance on train throughput can be made negligible by making the train long enough. Thus, we need only know the top speed and most wagon-heavy loco-to-wagon ratio that can achieve said top speed to compute the upper bound for train throughput.
Re: On the capacity of trains
Posted: Sun May 06, 2018 8:21 pm
by rgx
jcramner, this is brilliant stuff. I have observed and thought the same, so trying to limit the speeds of the trains, and also keeping the trains to the same fuel and size. Because maximum throughput also requires trains to have same speed and braking distance ideally.
Add to that that I like trains to be slow, accelerate slowly, and have long braking distance. I see no point in researching braking distance, the trains already outbrake a normal car. And accelerate quicker too.
It would have been great if max speed of trains could be set, to increase throughput. Now what I do is try to tune the length and locomotives/fuel to reach a nice speed, but it's very difficult, and leads to high fuel consumption. 1+8 trains on coal/wood works fine, max speed is around 155 km/h. But lower speed would have been nice, maybe 100 km/h for cargo trains.
Re: On the capacity of trains
Posted: Sun May 06, 2018 10:40 pm
by Frightning
Regarding my previous assertion about upper bound train throughput, I am going to assume that vehicle acceleration is implemented as a modifier to the train's power (so 250% vehicle acceleration means that the 600kW loco functions as though it had 2.5*600kW=1500kW=1.5MW of power). And with that assumption, compute the loco-to-wagon ratio, and from that, maximum train throughput.
Part 1: loco-to-wagon ratio
To begin, we take the formula provided by the OP in his/her original post:
Acceleration: speed at next tick = (speed - min(speed, friction / weight) + power / weight) * (1 - air_resistance / weight) {up to max_speed}
We note a few things:
speed is in tiles/tick
friction is 0.5*(# of locos+wagons)
weight is 200*(# of locos)+1000*(# of wagons)
power is 1500kW per loco (thanks to nuclear fuel, base is 600kW per loco), however, power in this formula is not in terms of kW, so we will need to deduce the constant for unit change to kW (which i will do using the old numbers I know for fuel with no speed/acceleration modifiers).
air_resistance is determined by lead loco or wagon (0.075 for a loco, 0.1 for a wagon)
max_speed is modified by nuclear fuel, to 115% of normal, which is 1.2*1.15=1.38 exactly.
Observe that beyond extremely slow speeds, min(speed, friction/weight) will always be speed because friction is small compared to weight, and is divided by said weight. Hence we can simplify the left part of the right side of the equation to be (speed-speed+power/weight), which becomes (power/weight). Similarly, for all but the shortest trains, air_resistance/weight will be extremely small (and tends to 0 as train length tends to infinity), hence we will treat it as 0, simplifying the right part to 1.
Lastly, the speed on the left of the equals sign should be none other than the max speed (after fuel modifier) of 1.38.
With these changes, we have obtained the simplified formula:
1.38=(power/weight)
Now, I recall that, with old numbers of 1.2 for max speed, and 600kW for power, we had an ideal ratio of 6 locos to 13 wagons. This gives the old version of the formula as:
1.2=(power/weight)
With weight=2000*6+1000*13=25000, and force=6*600kW=3600kW. Let power in the formula be C*force
1.2=(C*3600/25000)
We solve for C and obtain:
C=1.2*(25000/3600)=8.(3)=25/3
Plugging this back into the new formula, we obtain:
1.38=(25/3)*(power/weight)
(power/weight)=0.1656
Now, power=(# locos*1500kW), and weight=(#locos*2000+#wagons*1000)
This gives a linear system of equations, we solve that system as follows:
First, let P=power, L=number of locos, M=weight, and W=number of wagons.
Then the system is:
P/M=0.1656
P=1500*L
M=2000*L+1000*W
Notice we have 4 variables but only 3 equations. This is expected, our solution is actually a family of solutions in one parameter (how long the train will actually be), thus we seek to find the ratio between L and W and thus wish to expunge P and M from our equations.
We will do this by substituted the 2nd and 3rd equations into the first:
(1500L)/(2000L+1000W)=0.1656
Now we seek to form an expression on the left of the form L/W, with the right-side being only a constant.
Multiply both sides by denominator (of the left side)
1500L=0.1656(2000L+1000W)
Divide both sides by left side, obtaining 1 on the left
1=0.1656((2000L+1000W)/1500L)
Split fraction over common denominator
1=0.1656(2000L/1500L+1000W/1500L)
Simplify
1=0.1656((4/3)+(2W/3L))
Distribute
1=0.1656(4/3)+0.1656(2W/3L)
Subtract
1-0.1656(4/3)=0.1656(2W/3L)
0.7792=0.1656(2W/3L)
Divide
0.7792/0.1656=2W/3L
Rewrite left side by multiplying top and bottom by 10000 (so, by 10000/10000, a form of 1), re-express right side so that W/L is isolated
7792/1656=(2/3)*(W/L)
Multiply both sides by (3/2)
23376/3312=W/L
Reduce fraction to lowest terms
487/69=W/L
487 is prime, therefore this is in lowest terms. Thus the optimal loco-to-wagon ratio is 69 locos to 487 wagons (just over 7 wagons per loco).
Part 2: Maximum throughput
Armed with the new optimal ratio, we can straightforwardly compute train throughput (in wagons/sec) as follows:
Let S denote train speed in tiles/tick (which we know to be 1.38), R denote the proportion of the train that is wagons (which is 487/(69+487), by using loco-to-wagon ratio previously computed). Each loco and wagon is effectively 7 tiles long (6 for unit itself+1 unit for the coupling with the next loco or wagon) we will call this 7-tile distance a 'train unit'. There are 60 ticks in 1 second, so we will convert S to units of train units per second. 1.38 tiles/tick=1.38/7 train units/tick=60*1.38/7 train units/sec, which works out to
828/70=414/35=11.8(285714). Now, we multiply this result by the ratio R to obtain the wagons/sec value we desire.
S*R=(414/35)*(487/(69+487))=(414/35)*(487/556)=201668/19460=50417/4865=~10.363 wagons/sec
In terms of ores, which stack to 50, that works out to ~20,726.413 ores/sec (~20.7k ore/sec)
Re: On the capacity of trains
Posted: Mon May 07, 2018 10:11 am
by Bauer
jcranmer wrote:I honestly don't know why people are so surprised that higher speeds means lower throughput for trains. This is true in Factorio, as can be demonstrated both from theoretical terms as well as experimental terms, and it's true for real life trains.
And it's also true for Highways. Depending on driving culture (car-to-car distance, avg. acceleration, etc.) the max. throughput is at about 70-90 km/h. You can often observe that everyone is moving at that speed before the traffic breaks down completely.
Re: On the capacity of trains
Posted: Mon May 07, 2018 11:30 am
by mrvn
Lubricus wrote:I agree on that the junctions usually is the bottleneck.
With a perfect rail-network without crossings I suppose the inserters loading and unloading trains is the bottleneck, but that depends on how many station you cram onto a rail (is it possible with several train-stations without crossings?).
You can split a single rail line into 32 branches with a station at each. Then merge them back together into one line using circuit controlled signals for perfect timing . Now you have a nice little (hehe) in-line station that can manage one LC train every 73 ticks. Numbers may vary for longer trains.
Use that for the ore trains. Then for plates you only need half as much since they stack better. Half again for gears. Less for green circuits or steel. As you produce more complex products you quickly get into numbers where some junction bottleneck becomes irrelevant. You only need to keep the highest throughput items on non-crossing train networks.
Re: On the capacity of trains
Posted: Mon May 07, 2018 11:34 am
by mrvn
Bauer wrote:jcranmer wrote:I honestly don't know why people are so surprised that higher speeds means lower throughput for trains. This is true in Factorio, as can be demonstrated both from theoretical terms as well as experimental terms, and it's true for real life trains.
And it's also true for Highways. Depending on driving culture (car-to-car distance, avg. acceleration, etc.) the max. throughput is at about 70-90 km/h. You can often observe that everyone is moving at that speed before the traffic breaks down completely.
That's only because you don't have smart trains. A train wouldn't need to leave <breaking distance> space to the previous train. It only needs enough space so that if both trains break it won't bump into the previous train.
Re: On the capacity of trains
Posted: Mon May 07, 2018 1:18 pm
by bobucles
For a train to move at top speed, it needs to have an empty space in front of it for braking distance (you can see the empty gap if you turn on one of the debug options). When the braking distance hits a red light, the train has to slow down until it can change the light to yellow. That distance grows according to the square of the speed, while the time it takes to clear that distance only grows linearly with speed. Thus, the time interval between trains grows in proportion to train speed.
Oh yes, of course! I totally forgot that breaking distance was a thing. It effectively increases the length of the train and thus reduces the compression of cargo cars on the track. Less train compression means less throughput by a function that is speed^2, which is more powerful factor than the linear throughput increase of speed^1.
I have seen plenty of trains slow down when they reach the heavier portions of the track but didn't really think much about it. Now I see they were trying to reserve their braking distance just in case
Re: On the capacity of trains
Posted: Thu May 10, 2018 9:13 pm
by Zanthra
Once you have roboports, construction robots, and repair packs, could you use gates on an unsignaled rail system, and short trains (max length that won't destroy gates or rail cars when crashing at full speed), to prevent deadlocks and have trains queue by smashing into the gate or train ahead of them to avoid the braking distance problem? Is there any way to reliably tell if there is another train in an area without using circuit conditions from a rail signal?