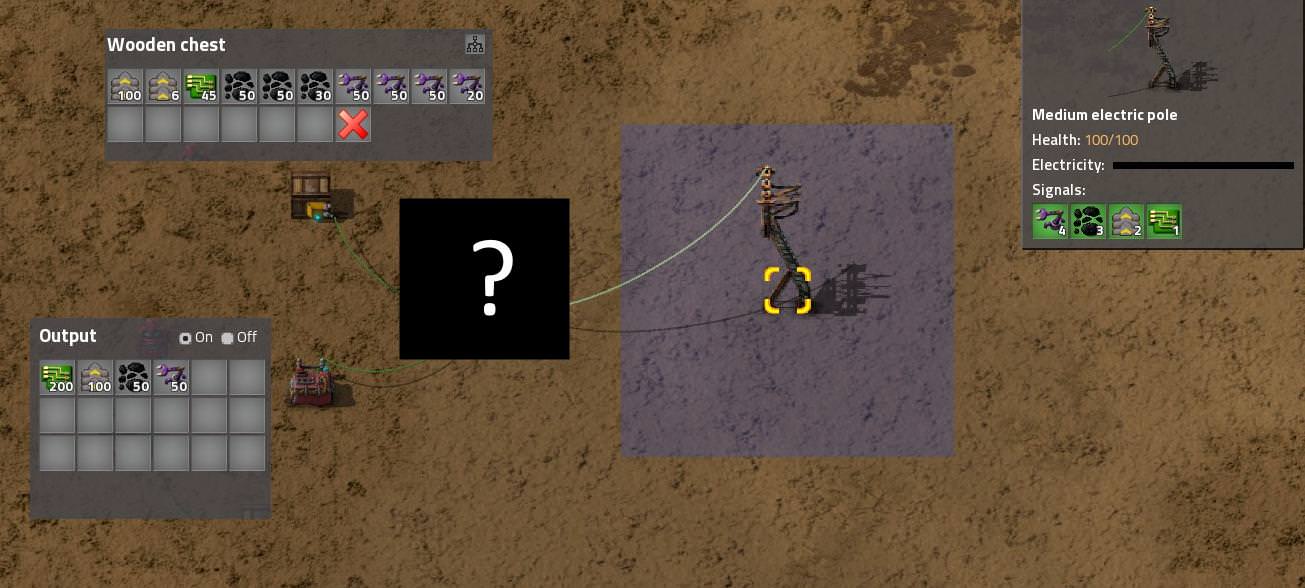
I came up with a solution, it's not pretty or compact and it delays the signal by 3 ticks buuut I guess it works. I dare anyone to come up with something better (because honestly this is kinda crap even by my standards).

Went with the filtering approach. The thing I'm standing next to is the wood chest with the items. The three lines of combinators represent 3 different stack sizes - 50, 100, 200. Items get filtered based on stack sizes via
this method (you select which belongs where in the constant combinator manually), then an arithmetic combinator divides them by the stack size, rounding down. This generally gives us an output 1 less than reality, so we calculate the remainder from division as well, and if that's more than 1, then that 1 is added to the final result. In normal operation you'd have 8 lines, one for each stack size.
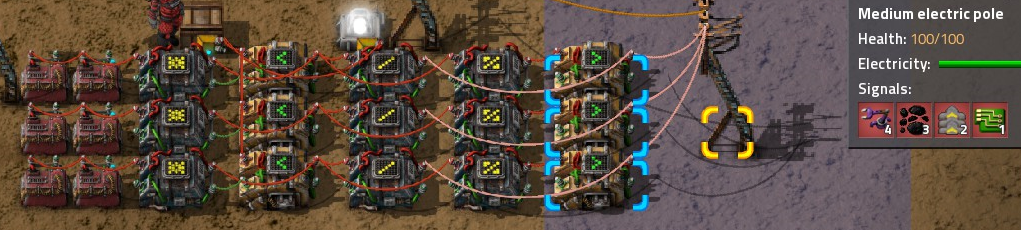
A more concise explanation of how a line of this works, going from left to right:
The constant combinators hold 1 of each item type for the given stack size. There's about 220 unique items in the game and one combinator can hold up to 18 unique items, meaning 8 rows of 2 is enough for every type (you'd probably need more for mods). I suspect you'd need more for items with stacks of 50 and 100 and less for 1 and 5, but whatever.
The first arithmetic multiplies Each item type from the constant combinators by -2147483648. This is technically unnecessary as you can set each item type to this value in the constant combinator, but whatever.
Next comes the decider. This checks if Each < 0, outputs Each. The wiring here is a little tricky - the chest is connected to the red input of the decider, where the previous arithmetic, the one with -2147483648 as its output, is connected to the green input of the decider. It's crucial that these don't mix, because the chest output goes across all lines. Now, the output of that same -2147483648 arithmetic is also connected to the output of the decider via red wire, where they get added together, filtering items for us via integer underflow magic.
This filtered signal is then passed to two arithmetic combinators. One divides it by the stack size of our line, for the 50 stack line that's i.e. Each/50, output Each. Now if we're dealing with 170 filter inserters, then the result will be 3 due to division always rounding down. This is no good, 170 filter inserters take up 4 slots. Hence the second arithmetic, also connected to the output of the filter. This one divides Each by 50 as well, except it only outputs the remainder as Each, that's the % sign thing (AKA modulo). In the case of filter inserters, that's going to be 20.
The remainder/modulo is then put through a decider that outputs 1 if Each > 0. In practical terms, this serves to count even partial stacks as stacks, because, as I said, the original divider doesn't count those. This is then added to the final result on the power pole. Tada.
To make a properly timed system you'd have to add an extra dummy combinator per line to delay the original signal by a tick due to the modulo shenanigans, so that'd be even less space/anything-efficient.
Drury wrote:but whatever.