quale wrote: ↑Wed Oct 25, 2023 2:11 pm
Funny you should mention RCT. [..] I learned about the latter part through Marcel Vos.
I see you are a connoisseur of the fine arts x) I'm tempted to think that a game from 1999 or so decided against using the square of acceleration deliberatly for perfomance reasons. I know factorio also does take some liberty with physics for air_resistance that doesn't apply to braking trains. I had heard of that corkscrew magic too, but to my memory it was a trick relying on the fact that you could make a loop with pieces whose lengh didn't added up, something like you were going more "down" than "up" as an Escher painting. I've heard of the calculator Marcel Vos made in RCT2 and was able to find the video but it's unclear if that is gravity of lengh or position function that is 'problematic'.
(
https://www.youtube.com/watch?v=EbjqWThzXME)
quale wrote: ↑Wed Oct 25, 2023 2:11 pm
There is no closed form for length. What matters for Factorio, though, is that you can set a length and it will behave as such. That length is defining. The position function is basically just flair. It will work fine as long as that function isn’t gravely off, such as by causing adjacent carriages to collide. Signal-less operation is likewise defined by those lengths that have been set. Long-term integration error is tiny in binary64 and affects different trains similarly. The visual requirements are much more stringent than that, yet are also easily met.
I did that one quite some time ago without knowing if it would work for long time :
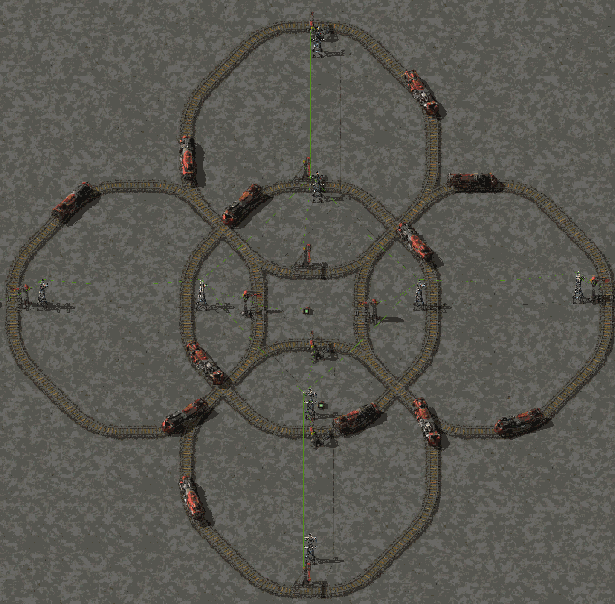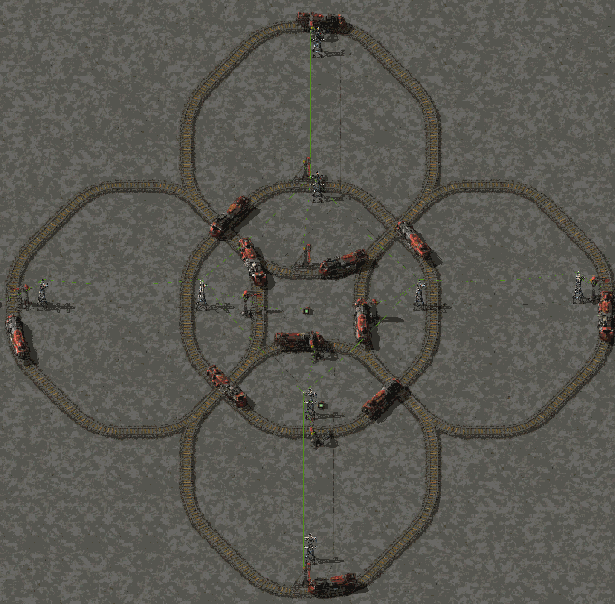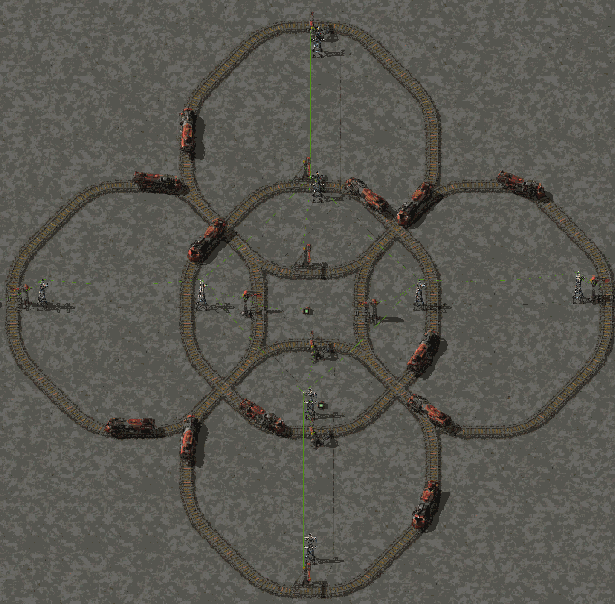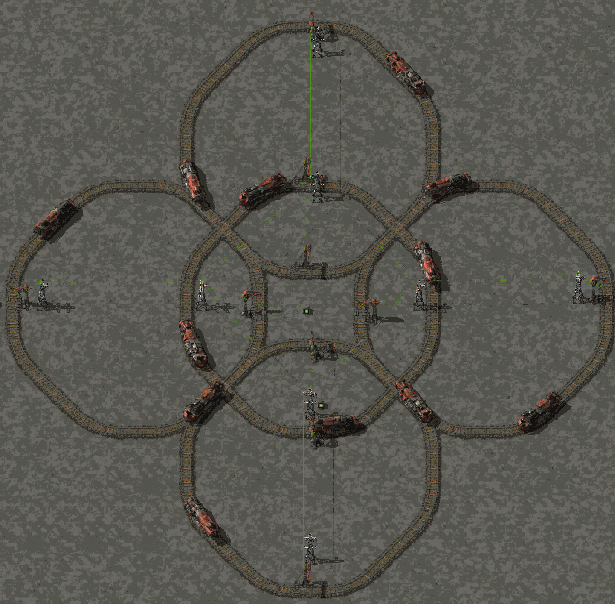
- atom4.gif (5.99 MiB) Viewed 3319 times
It relies on what you describe, the integration error affecting trains similarly i suppose. But knowing the exact time a train need to do 1 lap is knowing the period of the GIF or is knowing the frequency at which you can try to send a train through the existing rotating trains. Since the exact lengh of trains squircle in factorio are not transcendental, it is possible to find such period exactly in a finite amount of time ! It is yielding a squaring the circle problem equivalent

Synchronization in previous gif was done using combinators to turn all station on at the same time, but when building larger thing accross the map and several days i usually use a solar pannel to power a combinator at the exact same tick modulo 1 day. Mathing things out precisely could offer another tool to build those. The exact length are indeed enough, the position function is more curiosity

quale wrote: ↑Wed Oct 25, 2023 2:11 pm
Years ago I toyed a little with No Limits. I think it also used splines. I’d think that it would be much more stringent for that type of simulation, and it can afford to be. You can always subdivide a spline to get a more accurate length estimation or whatever you need. The smoothness can only be an asset to higher-order physics. The simulation doesn’t have to run hundreds of trains alongside a gigantic factory. If there are more steps to making it work the way it needs to, it can just take them, not to mention that there will be such steps regardless of the track’s representation at the level where I expect it to be.
I've heard of No Limits but i think it looked like this FVD++ (Force Vector Design) thing :
https://www.youtube.com/watch?v=o_cOiYa-0qM Where you can draw pieces of track from math functions as they say in first minutes of the video. Those track can then be imported in No Limits.
No Limits seem to indeed use splines a lot, but FVD i think ( it was long time ) allows to make different curves that may be more suited to the physics of real life (coaster) trains.
Khagan wrote: ↑Wed Oct 25, 2023 10:19 pm
Ironically, one of the places you
won't find splines is real-world roads and railways (I know nothing about rollercoasters). Real road and rail curves are circular arcs with (approximately) Euler spiral transitions.
Well nobody's perfect , rollercoasters i found are the main video game analog for adding the effect of gravity to trains in a fun way

They make up for fun curves like the Brachistochrone !
That's funny you mention Euler spiral transition, i've heard of them under the name clothoid, i didn't realize it was those used for real life railroad. But are you sure they are not splines ?
I found some article with :
Abstract. Highway and railway designers use clothoid splines (planar G1
curves consisting of straight line segments, circular arcs, and clothoid segments)
as center lines in route location. This paper considers the problem of finding a
clothoid spline transition spiral which joins two given points and matches given
curvatures and unit tangents at the two points. Conditions are given for the ex-
istence and uniqueness of the clothoid spline transition spirals, and algorithms
for finding them are outlined
https://www.ams.org/journals/mcom/1992- ... 4736-8.pdf
But i can't understand the math, that doesn't seem a topic that has been vulgarized a lot.
There are many many kind of splines, the cubic or bezier curves are just part of a larger group. I understood splines as a curve generation method and clothoid is a special curve where the angle changes in a linear fashion. I don't think they are both exclusive, but if i was to see the math that allow to create a spline to generate clothoids i wouldn't be able to recognize it maybe it's the math in the article i can't understand.
Maybe the way clothoid are approximated in real life is using spline that one can use in video games, that would be different i couldn't know maybe you are correct and those are not splines.
Thanks you for bringing this here, we still don't know what was refered to as "crazy math involving some gauge number of 35/64" by boskid, which is how the exact length of a curve rail was computed. So maybe the 1.1 curve rail length was computed using circular arcs with euler's spiral transition as a base for speed calculations.
The initial question is very difficult to answer with word, whereas a picture is much easier to take

